Note
Go to the end to download the full example code
3D plot projection types#
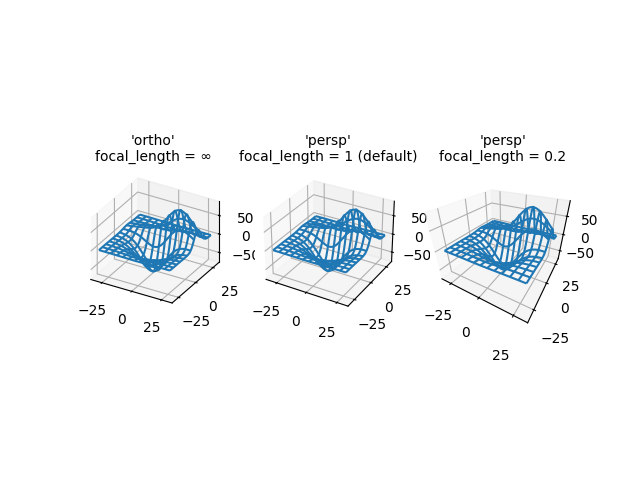
Demonstrates the different camera projections for 3D plots, and the effects of changing the focal length for a perspective projection. Note that Matplotlib corrects for the 'zoom' effect of changing the focal length.
The default focal length of 1 corresponds to a Field of View (FOV) of 90 deg. An increased focal length between 1 and infinity "flattens" the image, while a decreased focal length between 1 and 0 exaggerates the perspective and gives the image more apparent depth. In the limiting case, a focal length of infinity corresponds to an orthographic projection after correction of the zoom effect.
You can calculate focal length from a FOV via the equation:
\[1 / \tan (\mathrm{FOV} / 2)\]
Or vice versa:
\[\mathrm{FOV} = 2 \arctan (1 / \mathrm{focal length})\]
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
fig, axs = plt.subplots(1, 3, subplot_kw={'projection': '3d'})
# Get the test data
X, Y, Z = axes3d.get_test_data(0.05)
# Plot the data
for ax in axs:
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
# Set the orthographic projection.
axs[0].set_proj_type('ortho') # FOV = 0 deg
axs[0].set_title("'ortho'\nfocal_length = ∞", fontsize=10)
# Set the perspective projections
axs[1].set_proj_type('persp') # FOV = 90 deg
axs[1].set_title("'persp'\nfocal_length = 1 (default)", fontsize=10)
axs[2].set_proj_type('persp', focal_length=0.2) # FOV = 157.4 deg
axs[2].set_title("'persp'\nfocal_length = 0.2", fontsize=10)
plt.show()