Note
Go to the end to download the full example code
Colormap normalizations#
Demonstration of using norm to map colormaps onto data in non-linear ways.
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.colors as colors
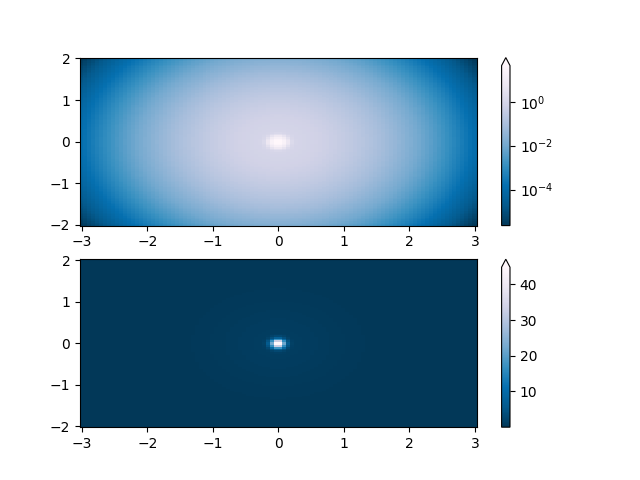
Lognorm: Instead of pcolor log10(Z1) you can have colorbars that have the exponential labels using a norm.
N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
# A low hump with a spike coming out of the top. Needs to have
# z/colour axis on a log scale, so we see both hump and spike.
# A linear scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolor(X, Y, Z,
norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
cmap='PuBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='max')
pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='max')
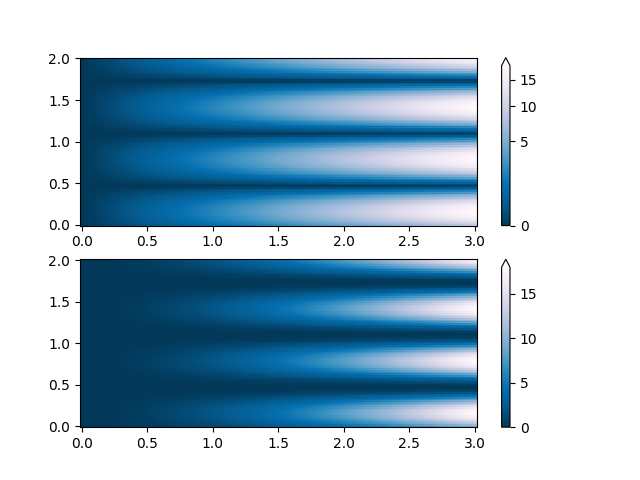
PowerNorm: Here a power-law trend in X partially obscures a rectified sine wave in Y. We can remove the power law using a PowerNorm.
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=1. / 2.),
cmap='PuBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='max')
pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='max')
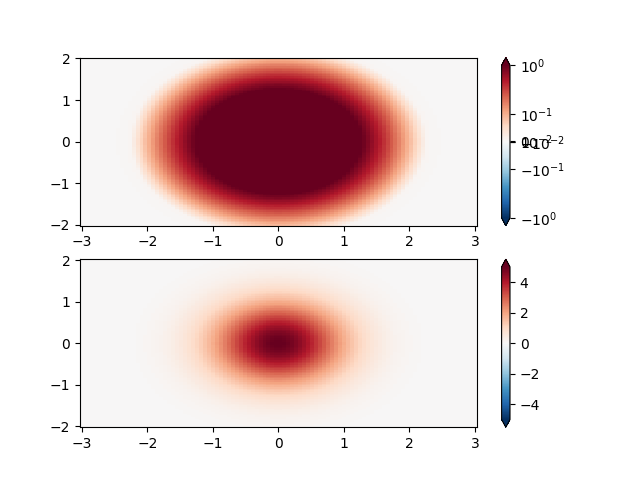
SymLogNorm: two humps, one negative and one positive, The positive with 5-times the amplitude. Linearly, you cannot see detail in the negative hump. Here we logarithmically scale the positive and negative data separately.
Note that colorbar labels do not come out looking very good.
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z = 5 * np.exp(-X**2 - Y**2)
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolormesh(X, Y, Z,
norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
vmin=-1.0, vmax=1.0, base=10),
cmap='RdBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='both')
pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z),
shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='both')
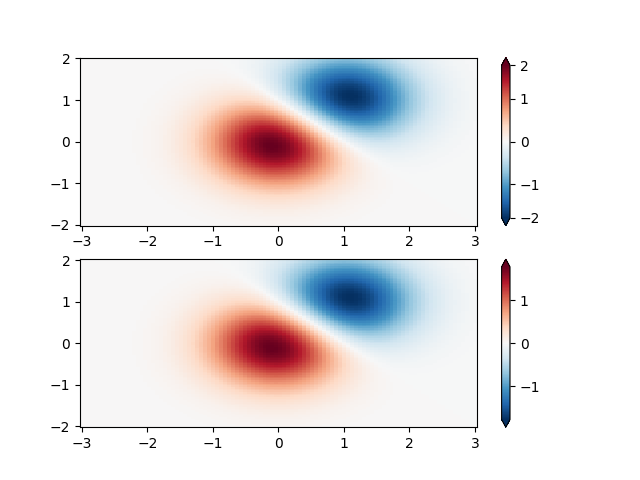
Custom Norm: An example with a customized normalization. This one uses the example above, and normalizes the negative data differently from the positive.
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2
# Example of making your own norm. Also see matplotlib.colors.
# From Joe Kington: This one gives two different linear ramps:
class MidpointNormalize(colors.Normalize):
def __init__(self, vmin=None, vmax=None, midpoint=None, clip=False):
self.midpoint = midpoint
super().__init__(vmin, vmax, clip)
def __call__(self, value, clip=None):
# I'm ignoring masked values and all kinds of edge cases to make a
# simple example...
x, y = [self.vmin, self.midpoint, self.vmax], [0, 0.5, 1]
return np.ma.masked_array(np.interp(value, x, y))
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolormesh(X, Y, Z,
norm=MidpointNormalize(midpoint=0.),
cmap='RdBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='both')
pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z),
shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='both')
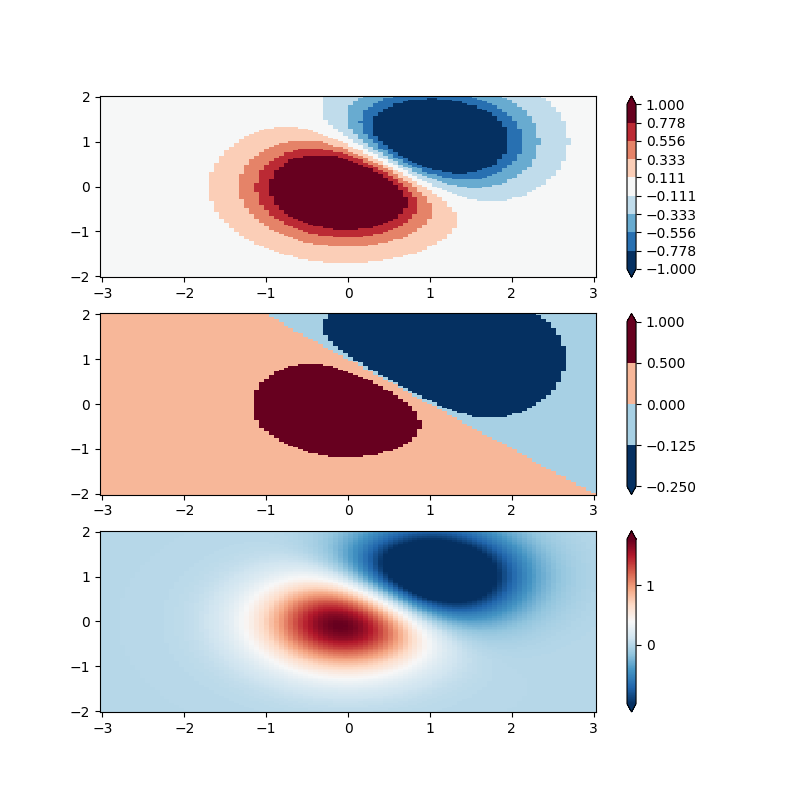
BoundaryNorm: For this one you provide the boundaries for your colors, and the Norm puts the first color in between the first pair, the second color between the second pair, etc.
fig, ax = plt.subplots(3, 1, figsize=(8, 8))
ax = ax.flatten()
# even bounds gives a contour-like effect
bounds = np.linspace(-1, 1, 10)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[0].pcolormesh(X, Y, Z,
norm=norm,
cmap='RdBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='both', orientation='vertical')
# uneven bounds changes the colormapping:
bounds = np.array([-0.25, -0.125, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
pcm = ax[2].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z1),
shading='nearest')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
plt.show()
Total running time of the script: (0 minutes 1.660 seconds)