Note
Go to the end to download the full example code
Contouring the solution space of optimizations#
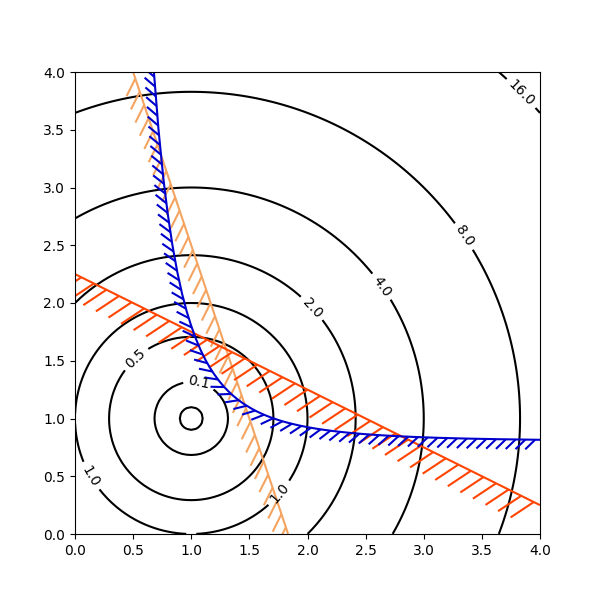
Contour plotting is particularly handy when illustrating the solution
space of optimization problems. Not only can axes.Axes.contour be
used to represent the topography of the objective function, it can be
used to generate boundary curves of the constraint functions. The
constraint lines can be drawn with
TickedStroke to distinguish the valid and
invalid sides of the constraint boundaries.
axes.Axes.contour generates curves with larger values to the left
of the contour. The angle parameter is measured zero ahead with
increasing values to the left. Consequently, when using
TickedStroke to illustrate a constraint in
a typical optimization problem, the angle should be set between
zero and 180 degrees.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import patheffects
fig, ax = plt.subplots(figsize=(6, 6))
nx = 101
ny = 105
# Set up survey vectors
xvec = np.linspace(0.001, 4.0, nx)
yvec = np.linspace(0.001, 4.0, ny)
# Set up survey matrices. Design disk loading and gear ratio.
x1, x2 = np.meshgrid(xvec, yvec)
# Evaluate some stuff to plot
obj = x1**2 + x2**2 - 2*x1 - 2*x2 + 2
g1 = -(3*x1 + x2 - 5.5)
g2 = -(x1 + 2*x2 - 4.5)
g3 = 0.8 + x1**-3 - x2
cntr = ax.contour(x1, x2, obj, [0.01, 0.1, 0.5, 1, 2, 4, 8, 16],
colors='black')
ax.clabel(cntr, fmt="%2.1f", use_clabeltext=True)
cg1 = ax.contour(x1, x2, g1, [0], colors='sandybrown')
plt.setp(cg1.collections,
path_effects=[patheffects.withTickedStroke(angle=135)])
cg2 = ax.contour(x1, x2, g2, [0], colors='orangered')
plt.setp(cg2.collections,
path_effects=[patheffects.withTickedStroke(angle=60, length=2)])
cg3 = ax.contour(x1, x2, g3, [0], colors='mediumblue')
plt.setp(cg3.collections,
path_effects=[patheffects.withTickedStroke(spacing=7)])
ax.set_xlim(0, 4)
ax.set_ylim(0, 4)
plt.show()