Note
Click here to download the full example code
Transformations Tutorial#
Like any graphics packages, Matplotlib is built on top of a transformation
framework to easily move between coordinate systems, the userland data
coordinate system, the axes coordinate system, the figure coordinate
system, and the display coordinate system. In 95% of your plotting, you
won't need to think about this, as it happens under the hood, but as you push
the limits of custom figure generation, it helps to have an understanding of
these objects, so you can reuse the existing transformations Matplotlib makes
available to you, or create your own (see matplotlib.transforms). The
table below summarizes some useful coordinate systems, a description of each
system, and the transformation object for going from each coordinate system to
the display coordinates. In the "Transformation Object" column, ax is a
Axes instance, fig is a
Figure instance, and subfigure is a
SubFigure instance.
Coordinate system |
Description |
Transformation object from system to display |
|---|---|---|
"data" |
The coordinate system of the data in the Axes. |
|
"axes" |
The coordinate system of the
|
|
"subfigure" |
The coordinate system of the
|
|
"figure" |
The coordinate system of the
|
|
"figure-inches" |
The coordinate system of the
|
|
"xaxis", "yaxis" |
Blended coordinate systems, using data coordinates on one direction and axes coordinates on the other. |
|
"display" |
The native coordinate system of the output ; (0, 0) is the bottom left of the window, and (width, height) is top right of the output in "display units". The exact interpretation of the units depends on the back end. For example it is pixels for Agg and points for svg/pdf. |
The Transform objects are naive to the source and
destination coordinate systems, however the objects referred to in the table
above are constructed to take inputs in their coordinate system, and transform
the input to the display coordinate system. That is why the display
coordinate system has None for the "Transformation Object" column -- it
already is in display coordinates. The naming and destination conventions
are an aid to keeping track of the available "standard" coordinate systems and
transforms.
The transformations also know how to invert themselves (via
Transform.inverted) to generate a transform from output coordinate system
back to the input coordinate system. For example, ax.transData converts
values in data coordinates to display coordinates and
ax.transData.inversed() is a matplotlib.transforms.Transform that
goes from display coordinates to data coordinates. This is particularly useful
when processing events from the user interface, which typically occur in
display space, and you want to know where the mouse click or key-press occurred
in your data coordinate system.
Note that specifying the position of Artists in display coordinates may
change their relative location if the dpi or size of the figure changes.
This can cause confusion when printing or changing screen resolution, because
the object can change location and size. Therefore, it is most common for
artists placed in an Axes or figure to have their transform set to something
other than the IdentityTransform(); the default when an artist
is added to an Axes using add_artist is for the transform to be
ax.transData so that you can work and think in data coordinates and let
Matplotlib take care of the transformation to display.
Data coordinates#
Let's start with the most commonly used coordinate, the data coordinate
system. Whenever you add data to the axes, Matplotlib updates the datalimits,
most commonly updated with the set_xlim() and
set_ylim() methods. For example, in the figure
below, the data limits stretch from 0 to 10 on the x-axis, and -1 to 1 on the
y-axis.
You can use the ax.transData instance to transform from your
data to your display coordinate system, either a single point or a
sequence of points as shown below:
In [14]: type(ax.transData)
Out[14]: <class 'matplotlib.transforms.CompositeGenericTransform'>
In [15]: ax.transData.transform((5, 0))
Out[15]: array([ 335.175, 247. ])
In [16]: ax.transData.transform([(5, 0), (1, 2)])
Out[16]:
array([[ 335.175, 247. ],
[ 132.435, 642.2 ]])
You can use the inverted()
method to create a transform which will take you from display to data
coordinates:
In [41]: inv = ax.transData.inverted()
In [42]: type(inv)
Out[42]: <class 'matplotlib.transforms.CompositeGenericTransform'>
In [43]: inv.transform((335.175, 247.))
Out[43]: array([ 5., 0.])
If your are typing along with this tutorial, the exact values of the display coordinates may differ if you have a different window size or dpi setting. Likewise, in the figure below, the display labeled points are probably not the same as in the ipython session because the documentation figure size defaults are different.
x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)
xdata, ydata = 5, 0
# This computing the transform now, if anything
# (figure size, dpi, axes placement, data limits, scales..)
# changes re-calling transform will get a different value.
xdisplay, ydisplay = ax.transData.transform((xdata, ydata))
bbox = dict(boxstyle="round", fc="0.8")
arrowprops = dict(
arrowstyle="->",
connectionstyle="angle,angleA=0,angleB=90,rad=10")
offset = 72
ax.annotate('data = (%.1f, %.1f)' % (xdata, ydata),
(xdata, ydata), xytext=(-2*offset, offset), textcoords='offset points',
bbox=bbox, arrowprops=arrowprops)
disp = ax.annotate('display = (%.1f, %.1f)' % (xdisplay, ydisplay),
(xdisplay, ydisplay), xytext=(0.5*offset, -offset),
xycoords='figure pixels',
textcoords='offset points',
bbox=bbox, arrowprops=arrowprops)
plt.show()
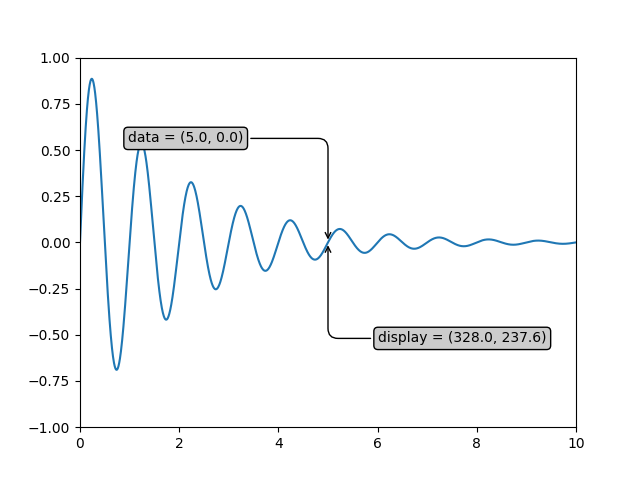
Warning
If you run the source code in the example above in a GUI backend,
you may also find that the two arrows for the data and display
annotations do not point to exactly the same point. This is because
the display point was computed before the figure was displayed, and
the GUI backend may slightly resize the figure when it is created.
The effect is more pronounced if you resize the figure yourself.
This is one good reason why you rarely want to work in display
space, but you can connect to the 'on_draw'
Event to update figure
coordinates on figure draws; see Event handling and picking.
When you change the x or y limits of your axes, the data limits are
updated so the transformation yields a new display point. Note that
when we just change the ylim, only the y-display coordinate is
altered, and when we change the xlim too, both are altered. More on
this later when we talk about the
Bbox.
In [54]: ax.transData.transform((5, 0))
Out[54]: array([ 335.175, 247. ])
In [55]: ax.set_ylim(-1, 2)
Out[55]: (-1, 2)
In [56]: ax.transData.transform((5, 0))
Out[56]: array([ 335.175 , 181.13333333])
In [57]: ax.set_xlim(10, 20)
Out[57]: (10, 20)
In [58]: ax.transData.transform((5, 0))
Out[58]: array([-171.675 , 181.13333333])
Axes coordinates#
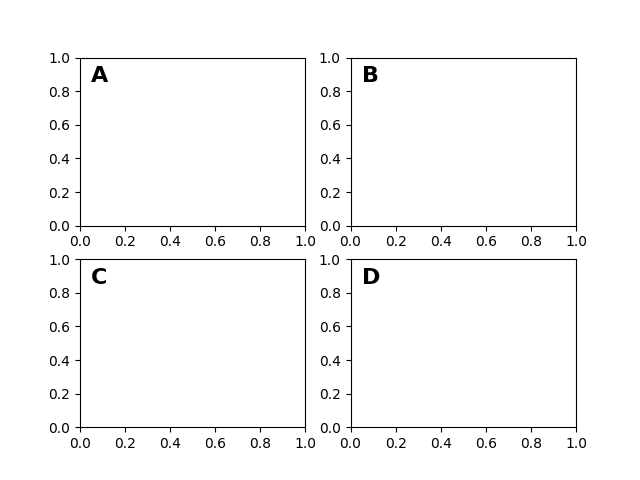
After the data coordinate system, axes is probably the second most useful coordinate system. Here the point (0, 0) is the bottom left of your axes or subplot, (0.5, 0.5) is the center, and (1.0, 1.0) is the top right. You can also refer to points outside the range, so (-0.1, 1.1) is to the left and above your axes. This coordinate system is extremely useful when placing text in your axes, because you often want a text bubble in a fixed, location, e.g., the upper left of the axes pane, and have that location remain fixed when you pan or zoom. Here is a simple example that creates four panels and labels them 'A', 'B', 'C', 'D' as you often see in journals.
fig = plt.figure()
for i, label in enumerate(('A', 'B', 'C', 'D')):
ax = fig.add_subplot(2, 2, i+1)
ax.text(0.05, 0.95, label, transform=ax.transAxes,
fontsize=16, fontweight='bold', va='top')
plt.show()
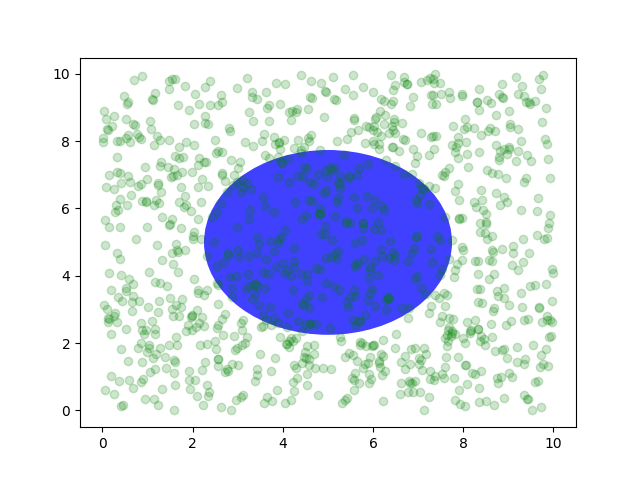
You can also make lines or patches in the axes coordinate system, but
this is less useful in my experience than using ax.transAxes for
placing text. Nonetheless, here is a silly example which plots some
random dots in data space, and overlays a semi-transparent
Circle centered in the middle of the axes
with a radius one quarter of the axes -- if your axes does not
preserve aspect ratio (see set_aspect()),
this will look like an ellipse. Use the pan/zoom tool to move around,
or manually change the data xlim and ylim, and you will see the data
move, but the circle will remain fixed because it is not in data
coordinates and will always remain at the center of the axes.
fig, ax = plt.subplots()
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y, 'go', alpha=0.2) # plot some data in data coordinates
circ = mpatches.Circle((0.5, 0.5), 0.25, transform=ax.transAxes,
facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()
Blended transformations#
Drawing in blended coordinate spaces which mix axes with data
coordinates is extremely useful, for example to create a horizontal
span which highlights some region of the y-data but spans across the
x-axis regardless of the data limits, pan or zoom level, etc. In fact
these blended lines and spans are so useful, we have built-in
functions to make them easy to plot (see
axhline(),
axvline(),
axhspan(),
axvspan()) but for didactic purposes we
will implement the horizontal span here using a blended
transformation. This trick only works for separable transformations,
like you see in normal Cartesian coordinate systems, but not on
inseparable transformations like the
PolarTransform.
import matplotlib.transforms as transforms
fig, ax = plt.subplots()
x = np.random.randn(1000)
ax.hist(x, 30)
ax.set_title(r'$\sigma=1 \/ \dots \/ \sigma=2$', fontsize=16)
# the x coords of this transformation are data, and the y coord are axes
trans = transforms.blended_transform_factory(
ax.transData, ax.transAxes)
# highlight the 1..2 stddev region with a span.
# We want x to be in data coordinates and y to span from 0..1 in axes coords.
rect = mpatches.Rectangle((1, 0), width=1, height=1, transform=trans,
color='yellow', alpha=0.5)
ax.add_patch(rect)
plt.show()
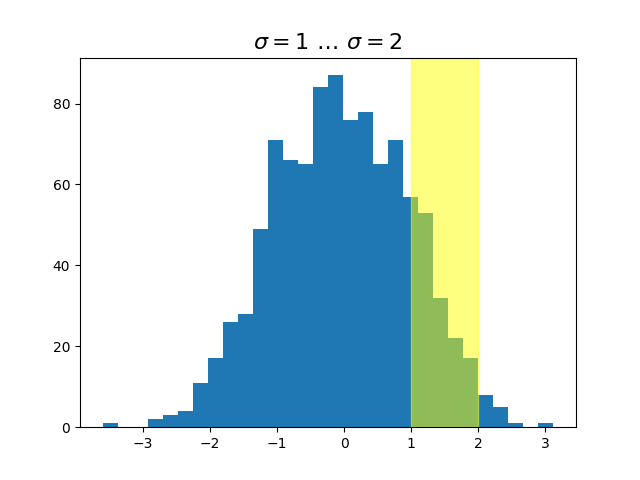
Note
The blended transformations where x is in data coords and y in axes
coordinates is so useful that we have helper methods to return the
versions Matplotlib uses internally for drawing ticks, ticklabels, etc.
The methods are matplotlib.axes.Axes.get_xaxis_transform() and
matplotlib.axes.Axes.get_yaxis_transform(). So in the example
above, the call to
blended_transform_factory() can be
replaced by get_xaxis_transform:
Plotting in physical coordinates#
Sometimes we want an object to be a certain physical size on the plot. Here we draw the same circle as above, but in physical coordinates. If done interactively, you can see that changing the size of the figure does not change the offset of the circle from the lower-left corner, does not change its size, and the circle remains a circle regardless of the aspect ratio of the axes.
fig, ax = plt.subplots(figsize=(5, 4))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2) # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()
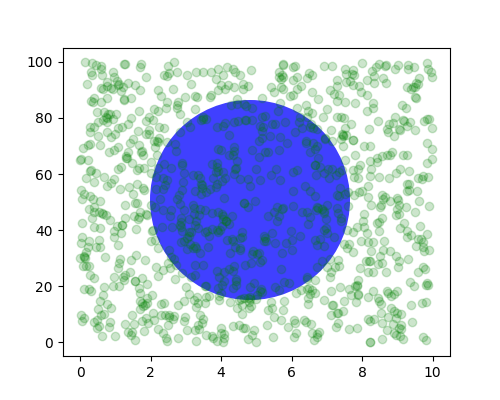
If we change the figure size, the circle does not change its absolute position and is cropped.
fig, ax = plt.subplots(figsize=(7, 2))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2) # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()
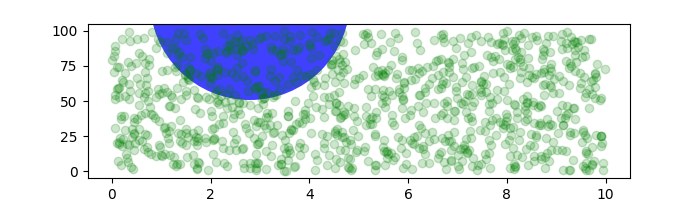
Another use is putting a patch with a set physical dimension around a
data point on the axes. Here we add together two transforms. The
first sets the scaling of how large the ellipse should be and the second
sets its position. The ellipse is then placed at the origin, and then
we use the helper transform ScaledTranslation
to move it
to the right place in the ax.transData coordinate system.
This helper is instantiated with:
trans = ScaledTranslation(xt, yt, scale_trans)
where xt and yt are the translation offsets, and scale_trans is a transformation which scales xt and yt at transformation time before applying the offsets.
Note the use of the plus operator on the transforms below.
This code says: first apply the scale transformation fig.dpi_scale_trans
to make the ellipse the proper size, but still centered at (0, 0),
and then translate the data to xdata[0] and ydata[0] in data space.
In interactive use, the ellipse stays the same size even if the axes limits are changed via zoom.
fig, ax = plt.subplots()
xdata, ydata = (0.2, 0.7), (0.5, 0.5)
ax.plot(xdata, ydata, "o")
ax.set_xlim((0, 1))
trans = (fig.dpi_scale_trans +
transforms.ScaledTranslation(xdata[0], ydata[0], ax.transData))
# plot an ellipse around the point that is 150 x 130 points in diameter...
circle = mpatches.Ellipse((0, 0), 150/72, 130/72, angle=40,
fill=None, transform=trans)
ax.add_patch(circle)
plt.show()
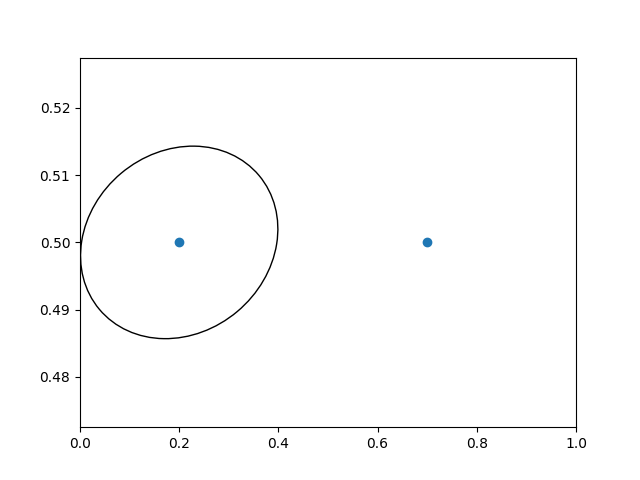
Note
The order of transformation matters. Here the ellipse
is given the right dimensions in display space first and then moved
in data space to the correct spot.
If we had done the ScaledTranslation first, then
xdata[0] and ydata[0] would
first be transformed to display coordinates ([ 358.4 475.2] on
a 200-dpi monitor) and then those coordinates
would be scaled by fig.dpi_scale_trans pushing the center of
the ellipse well off the screen (i.e. [ 71680. 95040.]).
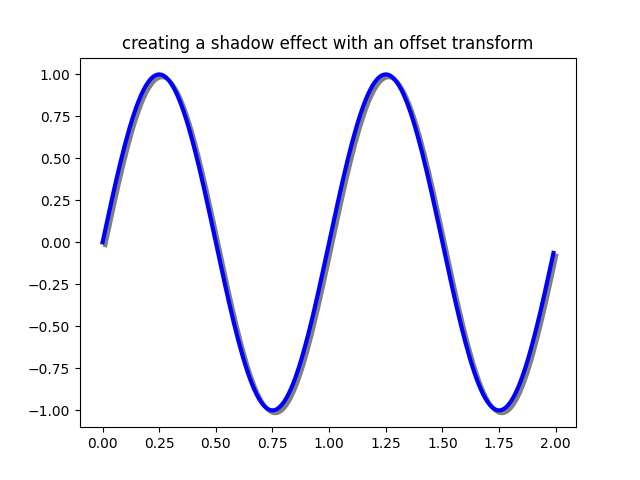
Using offset transforms to create a shadow effect#
Another use of ScaledTranslation is to create
a new transformation that is
offset from another transformation, e.g., to place one object shifted a
bit relative to another object. Typically, you want the shift to be in
some physical dimension, like points or inches rather than in data
coordinates, so that the shift effect is constant at different zoom
levels and dpi settings.
One use for an offset is to create a shadow effect, where you draw one object identical to the first just to the right of it, and just below it, adjusting the zorder to make sure the shadow is drawn first and then the object it is shadowing above it.
Here we apply the transforms in the opposite order to the use of
ScaledTranslation above. The plot is
first made in data coordinates (ax.transData) and then shifted by
dx and dy points using fig.dpi_scale_trans. (In typography,
a point is
1/72 inches, and by specifying your offsets in points, your figure
will look the same regardless of the dpi resolution it is saved in.)
fig, ax = plt.subplots()
# make a simple sine wave
x = np.arange(0., 2., 0.01)
y = np.sin(2*np.pi*x)
line, = ax.plot(x, y, lw=3, color='blue')
# shift the object over 2 points, and down 2 points
dx, dy = 2/72., -2/72.
offset = transforms.ScaledTranslation(dx, dy, fig.dpi_scale_trans)
shadow_transform = ax.transData + offset
# now plot the same data with our offset transform;
# use the zorder to make sure we are below the line
ax.plot(x, y, lw=3, color='gray',
transform=shadow_transform,
zorder=0.5*line.get_zorder())
ax.set_title('creating a shadow effect with an offset transform')
plt.show()
Note
The dpi and inches offset is a
common-enough use case that we have a special helper function to
create it in matplotlib.transforms.offset_copy(), which returns
a new transform with an added offset. So above we could have done:
shadow_transform = transforms.offset_copy(ax.transData,
fig, dx, dy, units='inches')
The transformation pipeline#
The ax.transData transform we have been working with in this
tutorial is a composite of three different transformations that
comprise the transformation pipeline from data -> display
coordinates. Michael Droettboom implemented the transformations
framework, taking care to provide a clean API that segregated the
nonlinear projections and scales that happen in polar and logarithmic
plots, from the linear affine transformations that happen when you pan
and zoom. There is an efficiency here, because you can pan and zoom
in your axes which affects the affine transformation, but you may not
need to compute the potentially expensive nonlinear scales or
projections on simple navigation events. It is also possible to
multiply affine transformation matrices together, and then apply them
to coordinates in one step. This is not true of all possible
transformations.
Here is how the ax.transData instance is defined in the basic
separable axis Axes class:
self.transData = self.transScale + (self.transLimits + self.transAxes)
We've been introduced to the transAxes instance above in
Axes coordinates, which maps the (0, 0), (1, 1) corners of the
axes or subplot bounding box to display space, so let's look at
these other two pieces.
self.transLimits is the transformation that takes you from
data to axes coordinates; i.e., it maps your view xlim and ylim
to the unit space of the axes (and transAxes then takes that unit
space to display space). We can see this in action here
In [80]: ax = plt.subplot()
In [81]: ax.set_xlim(0, 10)
Out[81]: (0, 10)
In [82]: ax.set_ylim(-1, 1)
Out[82]: (-1, 1)
In [84]: ax.transLimits.transform((0, -1))
Out[84]: array([ 0., 0.])
In [85]: ax.transLimits.transform((10, -1))
Out[85]: array([ 1., 0.])
In [86]: ax.transLimits.transform((10, 1))
Out[86]: array([ 1., 1.])
In [87]: ax.transLimits.transform((5, 0))
Out[87]: array([ 0.5, 0.5])
and we can use this same inverted transformation to go from the unit axes coordinates back to data coordinates.
In [90]: inv.transform((0.25, 0.25))
Out[90]: array([ 2.5, -0.5])
The final piece is the self.transScale attribute, which is
responsible for the optional non-linear scaling of the data, e.g., for
logarithmic axes. When an Axes is initially setup, this is just set to
the identity transform, since the basic Matplotlib axes has linear
scale, but when you call a logarithmic scaling function like
semilogx() or explicitly set the scale to
logarithmic with set_xscale(), then the
ax.transScale attribute is set to handle the nonlinear projection.
The scales transforms are properties of the respective xaxis and
yaxis Axis instances. For example, when
you call ax.set_xscale('log'), the xaxis updates its scale to a
matplotlib.scale.LogScale instance.
For non-separable axes the PolarAxes, there is one more piece to
consider, the projection transformation. The transData
matplotlib.projections.polar.PolarAxes is similar to that for
the typical separable matplotlib Axes, with one additional piece
transProjection:
self.transData = (
self.transScale + self.transShift + self.transProjection +
(self.transProjectionAffine + self.transWedge + self.transAxes))
transProjection handles the projection from the space,
e.g., latitude and longitude for map data, or radius and theta for polar
data, to a separable Cartesian coordinate system. There are several
projection examples in the matplotlib.projections package, and the
best way to learn more is to open the source for those packages and
see how to make your own, since Matplotlib supports extensible axes
and projections. Michael Droettboom has provided a nice tutorial
example of creating a Hammer projection axes; see
Custom projection.
Total running time of the script: ( 0 minutes 2.909 seconds)