Demonstration of using norm to map colormaps onto data in non-linear ways.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
from matplotlib.mlab import bivariate_normal
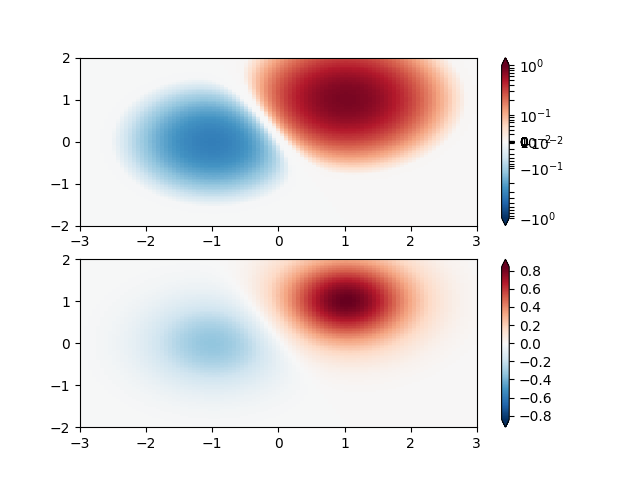
"""
SymLogNorm: two humps, one negative and one positive, The positive
with 5-times the amplitude. Linearly, you cannot see detail in the
negative hump. Here we logarithmically scale the positive and
negative data separately.
Note that colorbar labels do not come out looking very good.
"""
N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = (bivariate_normal(X, Y, 1., 1., 1.0, 1.0)**2 -
0.4 * bivariate_normal(X, Y, 1.0, 1.0, -1.0, 0.0)**2)
Z1 = Z1 / 0.03
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolormesh(X, Y, Z1,
norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
vmin=-1.0, vmax=1.0),
cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], extend='both')
pcm = ax[1].pcolormesh(X, Y, Z1, cmap='RdBu_r', vmin=-np.max(Z1))
fig.colorbar(pcm, ax=ax[1], extend='both')
plt.show()
Total running time of the script: ( 0 minutes 0.096 seconds)