Creating a colormap from a list of colors can be done with the from_list
method of LinearSegmentedColormap. You must pass a list of RGB tuples that
define the mixture of colors from 0 to 1.
It is also possible to create a custom mapping for a colormap. This is accomplished by creating dictionary that specifies how the RGB channels change from one end of the cmap to the other.
Example: suppose you want red to increase from 0 to 1 over the bottom half, green to do the same over the middle half, and blue over the top half. Then you would use:
cdict = {'red': ((0.0, 0.0, 0.0),
(0.5, 1.0, 1.0),
(1.0, 1.0, 1.0)),
'green': ((0.0, 0.0, 0.0),
(0.25, 0.0, 0.0),
(0.75, 1.0, 1.0),
(1.0, 1.0, 1.0)),
'blue': ((0.0, 0.0, 0.0),
(0.5, 0.0, 0.0),
(1.0, 1.0, 1.0))}
If, as in this example, there are no discontinuities in the r, g, and b components, then it is quite simple: the second and third element of each tuple, above, is the same–call it “y”. The first element (“x”) defines interpolation intervals over the full range of 0 to 1, and it must span that whole range. In other words, the values of x divide the 0-to-1 range into a set of segments, and y gives the end-point color values for each segment.
Now consider the green. cdict[‘green’] is saying that for 0 <= x <= 0.25, y is zero; no green. 0.25 < x <= 0.75, y varies linearly from 0 to 1. x > 0.75, y remains at 1, full green.
If there are discontinuities, then it is a little more complicated. Label the 3 elements in each row in the cdict entry for a given color as (x, y0, y1). Then for values of x between x[i] and x[i+1] the color value is interpolated between y1[i] and y0[i+1].
Going back to the cookbook example, look at cdict[‘red’]; because y0 != y1, it is saying that for x from 0 to 0.5, red increases from 0 to 1, but then it jumps down, so that for x from 0.5 to 1, red increases from 0.7 to 1. Green ramps from 0 to 1 as x goes from 0 to 0.5, then jumps back to 0, and ramps back to 1 as x goes from 0.5 to 1.:
row i: x y0 y1
/
/
row i+1: x y0 y1
Above is an attempt to show that for x in the range x[i] to x[i+1], the interpolation is between y1[i] and y0[i+1]. So, y0[0] and y1[-1] are never used.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
# Make some illustrative fake data:
x = np.arange(0, np.pi, 0.1)
y = np.arange(0, 2 * np.pi, 0.1)
X, Y = np.meshgrid(x, y)
Z = np.cos(X) * np.sin(Y) * 10
— Colormaps from a list —
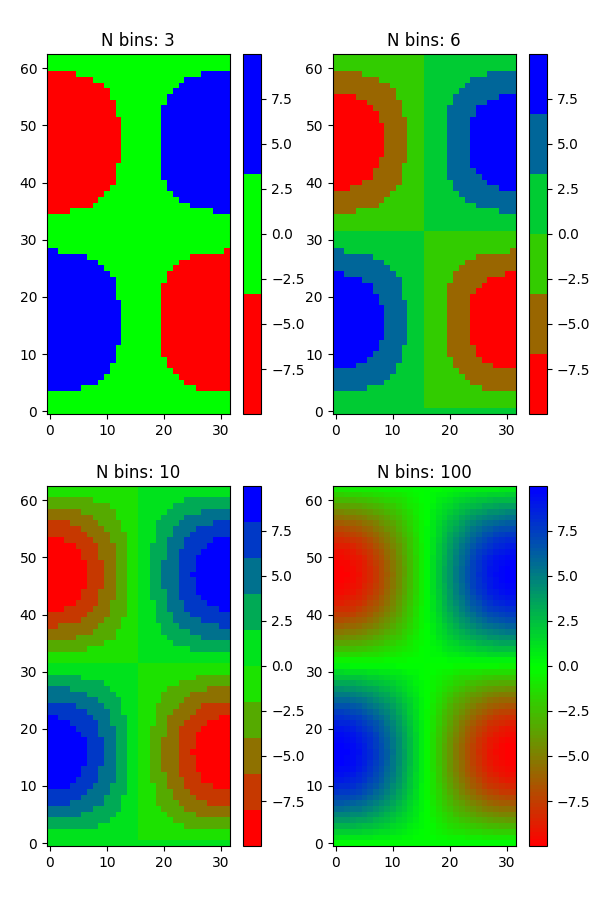
colors = [(1, 0, 0), (0, 1, 0), (0, 0, 1)] # R -> G -> B
n_bins = [3, 6, 10, 100] # Discretizes the interpolation into bins
cmap_name = 'my_list'
fig, axs = plt.subplots(2, 2, figsize=(6, 9))
fig.subplots_adjust(left=0.02, bottom=0.06, right=0.95, top=0.94, wspace=0.05)
for n_bin, ax in zip(n_bins, axs.ravel()):
# Create the colormap
cm = LinearSegmentedColormap.from_list(
cmap_name, colors, N=n_bin)
# Fewer bins will result in "coarser" colomap interpolation
im = ax.imshow(Z, interpolation='nearest', origin='lower', cmap=cm)
ax.set_title("N bins: %s" % n_bin)
fig.colorbar(im, ax=ax)
— Custom colormaps —
cdict1 = {'red': ((0.0, 0.0, 0.0),
(0.5, 0.0, 0.1),
(1.0, 1.0, 1.0)),
'green': ((0.0, 0.0, 0.0),
(1.0, 0.0, 0.0)),
'blue': ((0.0, 0.0, 1.0),
(0.5, 0.1, 0.0),
(1.0, 0.0, 0.0))
}
cdict2 = {'red': ((0.0, 0.0, 0.0),
(0.5, 0.0, 1.0),
(1.0, 0.1, 1.0)),
'green': ((0.0, 0.0, 0.0),
(1.0, 0.0, 0.0)),
'blue': ((0.0, 0.0, 0.1),
(0.5, 1.0, 0.0),
(1.0, 0.0, 0.0))
}
cdict3 = {'red': ((0.0, 0.0, 0.0),
(0.25, 0.0, 0.0),
(0.5, 0.8, 1.0),
(0.75, 1.0, 1.0),
(1.0, 0.4, 1.0)),
'green': ((0.0, 0.0, 0.0),
(0.25, 0.0, 0.0),
(0.5, 0.9, 0.9),
(0.75, 0.0, 0.0),
(1.0, 0.0, 0.0)),
'blue': ((0.0, 0.0, 0.4),
(0.25, 1.0, 1.0),
(0.5, 1.0, 0.8),
(0.75, 0.0, 0.0),
(1.0, 0.0, 0.0))
}
# Make a modified version of cdict3 with some transparency
# in the middle of the range.
cdict4 = cdict3.copy()
cdict4['alpha'] = ((0.0, 1.0, 1.0),
# (0.25,1.0, 1.0),
(0.5, 0.3, 0.3),
# (0.75,1.0, 1.0),
(1.0, 1.0, 1.0))
Now we will use this example to illustrate 3 ways of handling custom colormaps. First, the most direct and explicit:
blue_red1 = LinearSegmentedColormap('BlueRed1', cdict1)
Second, create the map explicitly and register it. Like the first method, this method works with any kind of Colormap, not just a LinearSegmentedColormap:
blue_red2 = LinearSegmentedColormap('BlueRed2', cdict2)
plt.register_cmap(cmap=blue_red2)
Third, for LinearSegmentedColormap only, leave everything to register_cmap:
plt.register_cmap(name='BlueRed3', data=cdict3) # optional lut kwarg
plt.register_cmap(name='BlueRedAlpha', data=cdict4)
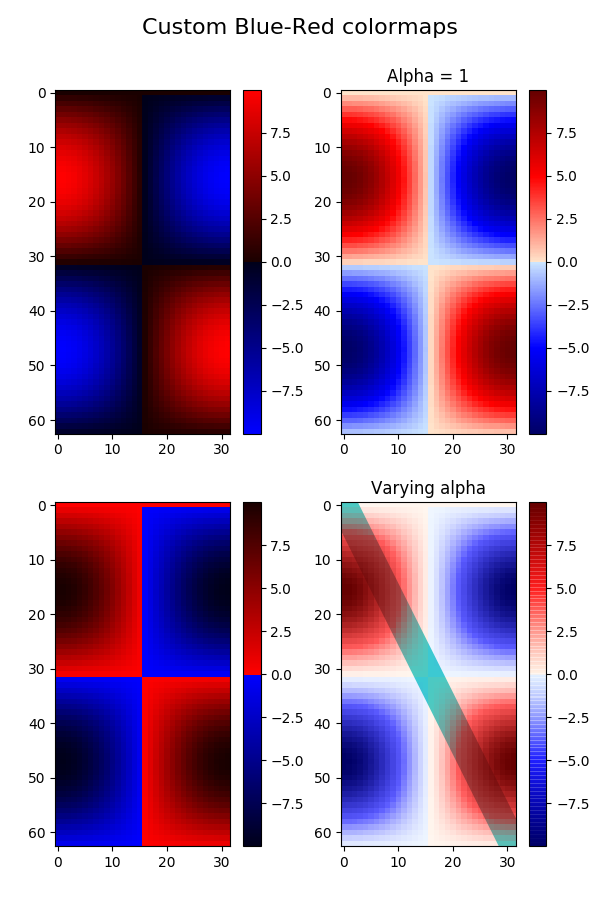
Make the figure:
fig, axs = plt.subplots(2, 2, figsize=(6, 9))
fig.subplots_adjust(left=0.02, bottom=0.06, right=0.95, top=0.94, wspace=0.05)
# Make 4 subplots:
im1 = axs[0, 0].imshow(Z, interpolation='nearest', cmap=blue_red1)
fig.colorbar(im1, ax=axs[0, 0])
cmap = plt.get_cmap('BlueRed2')
im2 = axs[1, 0].imshow(Z, interpolation='nearest', cmap=cmap)
fig.colorbar(im2, ax=axs[1, 0])
# Now we will set the third cmap as the default. One would
# not normally do this in the middle of a script like this;
# it is done here just to illustrate the method.
plt.rcParams['image.cmap'] = 'BlueRed3'
im3 = axs[0, 1].imshow(Z, interpolation='nearest')
fig.colorbar(im3, ax=axs[0, 1])
axs[0, 1].set_title("Alpha = 1")
# Or as yet another variation, we can replace the rcParams
# specification *before* the imshow with the following *after*
# imshow.
# This sets the new default *and* sets the colormap of the last
# image-like item plotted via pyplot, if any.
#
# Draw a line with low zorder so it will be behind the image.
axs[1, 1].plot([0, 10 * np.pi], [0, 20 * np.pi], color='c', lw=20, zorder=-1)
im4 = axs[1, 1].imshow(Z, interpolation='nearest')
fig.colorbar(im4, ax=axs[1, 1])
# Here it is: changing the colormap for the current image and its
# colorbar after they have been plotted.
im4.set_cmap('BlueRedAlpha')
axs[1, 1].set_title("Varying alpha")
#
fig.suptitle('Custom Blue-Red colormaps', fontsize=16)
fig.subplots_adjust(top=0.9)
plt.show()
Total running time of the script: ( 0 minutes 0.369 seconds)