
(Source code, png, pdf)
"""
===========================================================
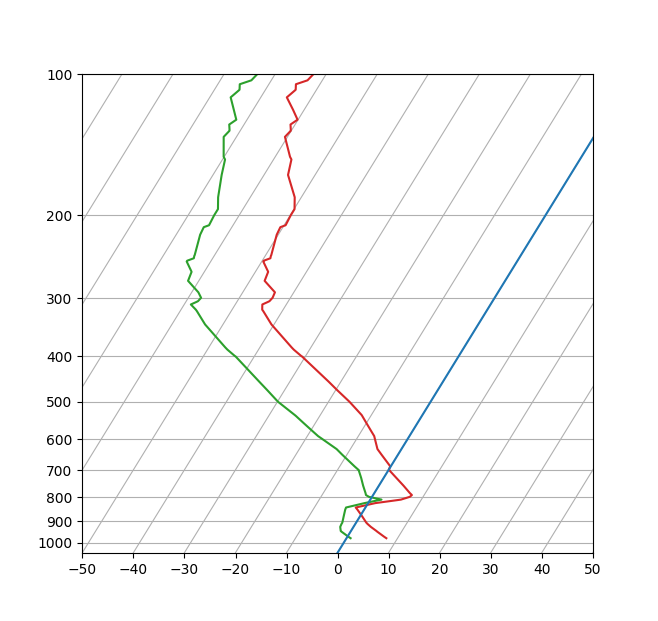
SkewT-logP diagram: using transforms and custom projections
===========================================================
This serves as an intensive exercise of matplotlib's transforms and custom
projection API. This example produces a so-called SkewT-logP diagram, which is
a common plot in meteorology for displaying vertical profiles of temperature.
As far as matplotlib is concerned, the complexity comes from having X and Y
axes that are not orthogonal. This is handled by including a skew component to
the basic Axes transforms. Additional complexity comes in handling the fact
that the upper and lower X-axes have different data ranges, which necessitates
a bunch of custom classes for ticks,spines, and the axis to handle this.
"""
from matplotlib.axes import Axes
import matplotlib.transforms as transforms
import matplotlib.axis as maxis
import matplotlib.spines as mspines
from matplotlib.projections import register_projection
# The sole purpose of this class is to look at the upper, lower, or total
# interval as appropriate and see what parts of the tick to draw, if any.
class SkewXTick(maxis.XTick):
def update_position(self, loc):
# This ensures that the new value of the location is set before
# any other updates take place
self._loc = loc
super(SkewXTick, self).update_position(loc)
def _has_default_loc(self):
return self.get_loc() is None
def _need_lower(self):
return (self._has_default_loc() or
transforms.interval_contains(self.axes.lower_xlim,
self.get_loc()))
def _need_upper(self):
return (self._has_default_loc() or
transforms.interval_contains(self.axes.upper_xlim,
self.get_loc()))
@property
def gridOn(self):
return (self._gridOn and (self._has_default_loc() or
transforms.interval_contains(self.get_view_interval(),
self.get_loc())))
@gridOn.setter
def gridOn(self, value):
self._gridOn = value
@property
def tick1On(self):
return self._tick1On and self._need_lower()
@tick1On.setter
def tick1On(self, value):
self._tick1On = value
@property
def label1On(self):
return self._label1On and self._need_lower()
@label1On.setter
def label1On(self, value):
self._label1On = value
@property
def tick2On(self):
return self._tick2On and self._need_upper()
@tick2On.setter
def tick2On(self, value):
self._tick2On = value
@property
def label2On(self):
return self._label2On and self._need_upper()
@label2On.setter
def label2On(self, value):
self._label2On = value
def get_view_interval(self):
return self.axes.xaxis.get_view_interval()
# This class exists to provide two separate sets of intervals to the tick,
# as well as create instances of the custom tick
class SkewXAxis(maxis.XAxis):
def _get_tick(self, major):
return SkewXTick(self.axes, None, '', major=major)
def get_view_interval(self):
return self.axes.upper_xlim[0], self.axes.lower_xlim[1]
# This class exists to calculate the separate data range of the
# upper X-axis and draw the spine there. It also provides this range
# to the X-axis artist for ticking and gridlines
class SkewSpine(mspines.Spine):
def _adjust_location(self):
pts = self._path.vertices
if self.spine_type == 'top':
pts[:, 0] = self.axes.upper_xlim
else:
pts[:, 0] = self.axes.lower_xlim
# This class handles registration of the skew-xaxes as a projection as well
# as setting up the appropriate transformations. It also overrides standard
# spines and axes instances as appropriate.
class SkewXAxes(Axes):
# The projection must specify a name. This will be used be the
# user to select the projection, i.e. ``subplot(111,
# projection='skewx')``.
name = 'skewx'
def _init_axis(self):
# Taken from Axes and modified to use our modified X-axis
self.xaxis = SkewXAxis(self)
self.spines['top'].register_axis(self.xaxis)
self.spines['bottom'].register_axis(self.xaxis)
self.yaxis = maxis.YAxis(self)
self.spines['left'].register_axis(self.yaxis)
self.spines['right'].register_axis(self.yaxis)
def _gen_axes_spines(self):
spines = {'top': SkewSpine.linear_spine(self, 'top'),
'bottom': mspines.Spine.linear_spine(self, 'bottom'),
'left': mspines.Spine.linear_spine(self, 'left'),
'right': mspines.Spine.linear_spine(self, 'right')}
return spines
def _set_lim_and_transforms(self):
"""
This is called once when the plot is created to set up all the
transforms for the data, text and grids.
"""
rot = 30
# Get the standard transform setup from the Axes base class
Axes._set_lim_and_transforms(self)
# Need to put the skew in the middle, after the scale and limits,
# but before the transAxes. This way, the skew is done in Axes
# coordinates thus performing the transform around the proper origin
# We keep the pre-transAxes transform around for other users, like the
# spines for finding bounds
self.transDataToAxes = self.transScale + \
self.transLimits + transforms.Affine2D().skew_deg(rot, 0)
# Create the full transform from Data to Pixels
self.transData = self.transDataToAxes + self.transAxes
# Blended transforms like this need to have the skewing applied using
# both axes, in axes coords like before.
self._xaxis_transform = (transforms.blended_transform_factory(
self.transScale + self.transLimits,
transforms.IdentityTransform()) +
transforms.Affine2D().skew_deg(rot, 0)) + self.transAxes
@property
def lower_xlim(self):
return self.axes.viewLim.intervalx
@property
def upper_xlim(self):
pts = [[0., 1.], [1., 1.]]
return self.transDataToAxes.inverted().transform(pts)[:, 0]
# Now register the projection with matplotlib so the user can select
# it.
register_projection(SkewXAxes)
if __name__ == '__main__':
# Now make a simple example using the custom projection.
from matplotlib.ticker import (MultipleLocator, NullFormatter,
ScalarFormatter)
import matplotlib.pyplot as plt
from six import StringIO
import numpy as np
# Some examples data
data_txt = '''
978.0 345 7.8 0.8 61 4.16 325 14 282.7 294.6 283.4
971.0 404 7.2 0.2 61 4.01 327 17 282.7 294.2 283.4
946.7 610 5.2 -1.8 61 3.56 335 26 282.8 293.0 283.4
944.0 634 5.0 -2.0 61 3.51 336 27 282.8 292.9 283.4
925.0 798 3.4 -2.6 65 3.43 340 32 282.8 292.7 283.4
911.8 914 2.4 -2.7 69 3.46 345 37 282.9 292.9 283.5
906.0 966 2.0 -2.7 71 3.47 348 39 283.0 293.0 283.6
877.9 1219 0.4 -3.2 77 3.46 0 48 283.9 293.9 284.5
850.0 1478 -1.3 -3.7 84 3.44 0 47 284.8 294.8 285.4
841.0 1563 -1.9 -3.8 87 3.45 358 45 285.0 295.0 285.6
823.0 1736 1.4 -0.7 86 4.44 353 42 290.3 303.3 291.0
813.6 1829 4.5 1.2 80 5.17 350 40 294.5 309.8 295.4
809.0 1875 6.0 2.2 77 5.57 347 39 296.6 313.2 297.6
798.0 1988 7.4 -0.6 57 4.61 340 35 299.2 313.3 300.1
791.0 2061 7.6 -1.4 53 4.39 335 33 300.2 313.6 301.0
783.9 2134 7.0 -1.7 54 4.32 330 31 300.4 313.6 301.2
755.1 2438 4.8 -3.1 57 4.06 300 24 301.2 313.7 301.9
727.3 2743 2.5 -4.4 60 3.81 285 29 301.9 313.8 302.6
700.5 3048 0.2 -5.8 64 3.57 275 31 302.7 313.8 303.3
700.0 3054 0.2 -5.8 64 3.56 280 31 302.7 313.8 303.3
698.0 3077 0.0 -6.0 64 3.52 280 31 302.7 313.7 303.4
687.0 3204 -0.1 -7.1 59 3.28 281 31 304.0 314.3 304.6
648.9 3658 -3.2 -10.9 55 2.59 285 30 305.5 313.8 305.9
631.0 3881 -4.7 -12.7 54 2.29 289 33 306.2 313.6 306.6
600.7 4267 -6.4 -16.7 44 1.73 295 39 308.6 314.3 308.9
592.0 4381 -6.9 -17.9 41 1.59 297 41 309.3 314.6 309.6
577.6 4572 -8.1 -19.6 39 1.41 300 44 310.1 314.9 310.3
555.3 4877 -10.0 -22.3 36 1.16 295 39 311.3 315.3 311.5
536.0 5151 -11.7 -24.7 33 0.97 304 39 312.4 315.8 312.6
533.8 5182 -11.9 -25.0 33 0.95 305 39 312.5 315.8 312.7
500.0 5680 -15.9 -29.9 29 0.64 290 44 313.6 315.9 313.7
472.3 6096 -19.7 -33.4 28 0.49 285 46 314.1 315.8 314.1
453.0 6401 -22.4 -36.0 28 0.39 300 50 314.4 315.8 314.4
400.0 7310 -30.7 -43.7 27 0.20 285 44 315.0 315.8 315.0
399.7 7315 -30.8 -43.8 27 0.20 285 44 315.0 315.8 315.0
387.0 7543 -33.1 -46.1 26 0.16 281 47 314.9 315.5 314.9
382.7 7620 -33.8 -46.8 26 0.15 280 48 315.0 315.6 315.0
342.0 8398 -40.5 -53.5 23 0.08 293 52 316.1 316.4 316.1
320.4 8839 -43.7 -56.7 22 0.06 300 54 317.6 317.8 317.6
318.0 8890 -44.1 -57.1 22 0.05 301 55 317.8 318.0 317.8
310.0 9060 -44.7 -58.7 19 0.04 304 61 319.2 319.4 319.2
306.1 9144 -43.9 -57.9 20 0.05 305 63 321.5 321.7 321.5
305.0 9169 -43.7 -57.7 20 0.05 303 63 322.1 322.4 322.1
300.0 9280 -43.5 -57.5 20 0.05 295 64 323.9 324.2 323.9
292.0 9462 -43.7 -58.7 17 0.05 293 67 326.2 326.4 326.2
276.0 9838 -47.1 -62.1 16 0.03 290 74 326.6 326.7 326.6
264.0 10132 -47.5 -62.5 16 0.03 288 79 330.1 330.3 330.1
251.0 10464 -49.7 -64.7 16 0.03 285 85 331.7 331.8 331.7
250.0 10490 -49.7 -64.7 16 0.03 285 85 332.1 332.2 332.1
247.0 10569 -48.7 -63.7 16 0.03 283 88 334.7 334.8 334.7
244.0 10649 -48.9 -63.9 16 0.03 280 91 335.6 335.7 335.6
243.3 10668 -48.9 -63.9 16 0.03 280 91 335.8 335.9 335.8
220.0 11327 -50.3 -65.3 15 0.03 280 85 343.5 343.6 343.5
212.0 11569 -50.5 -65.5 15 0.03 280 83 346.8 346.9 346.8
210.0 11631 -49.7 -64.7 16 0.03 280 83 349.0 349.1 349.0
200.0 11950 -49.9 -64.9 15 0.03 280 80 353.6 353.7 353.6
194.0 12149 -49.9 -64.9 15 0.03 279 78 356.7 356.8 356.7
183.0 12529 -51.3 -66.3 15 0.03 278 75 360.4 360.5 360.4
164.0 13233 -55.3 -68.3 18 0.02 277 69 365.2 365.3 365.2
152.0 13716 -56.5 -69.5 18 0.02 275 65 371.1 371.2 371.1
150.0 13800 -57.1 -70.1 18 0.02 275 64 371.5 371.6 371.5
136.0 14414 -60.5 -72.5 19 0.02 268 54 376.0 376.1 376.0
132.0 14600 -60.1 -72.1 19 0.02 265 51 380.0 380.1 380.0
131.4 14630 -60.2 -72.2 19 0.02 265 51 380.3 380.4 380.3
128.0 14792 -60.9 -72.9 19 0.02 266 50 381.9 382.0 381.9
125.0 14939 -60.1 -72.1 19 0.02 268 49 385.9 386.0 385.9
119.0 15240 -62.2 -73.8 20 0.01 270 48 387.4 387.5 387.4
112.0 15616 -64.9 -75.9 21 0.01 265 53 389.3 389.3 389.3
108.0 15838 -64.1 -75.1 21 0.01 265 58 394.8 394.9 394.8
107.8 15850 -64.1 -75.1 21 0.01 265 58 395.0 395.1 395.0
105.0 16010 -64.7 -75.7 21 0.01 272 50 396.9 396.9 396.9
103.0 16128 -62.9 -73.9 21 0.02 277 45 402.5 402.6 402.5
100.0 16310 -62.5 -73.5 21 0.02 285 36 406.7 406.8 406.7
'''
# Parse the data
sound_data = StringIO(data_txt)
p, h, T, Td = np.loadtxt(sound_data, usecols=range(0, 4), unpack=True)
# Create a new figure. The dimensions here give a good aspect ratio
fig = plt.figure(figsize=(6.5875, 6.2125))
ax = fig.add_subplot(111, projection='skewx')
plt.grid(True)
# Plot the data using normal plotting functions, in this case using
# log scaling in Y, as dictated by the typical meteorological plot
ax.semilogy(T, p, color='C3')
ax.semilogy(Td, p, color='C2')
# An example of a slanted line at constant X
l = ax.axvline(0, color='C0')
# Disables the log-formatting that comes with semilogy
ax.yaxis.set_major_formatter(ScalarFormatter())
ax.yaxis.set_minor_formatter(NullFormatter())
ax.set_yticks(np.linspace(100, 1000, 10))
ax.set_ylim(1050, 100)
ax.xaxis.set_major_locator(MultipleLocator(10))
ax.set_xlim(-50, 50)
plt.show()
Keywords: python, matplotlib, pylab, example, codex (see Search examples)