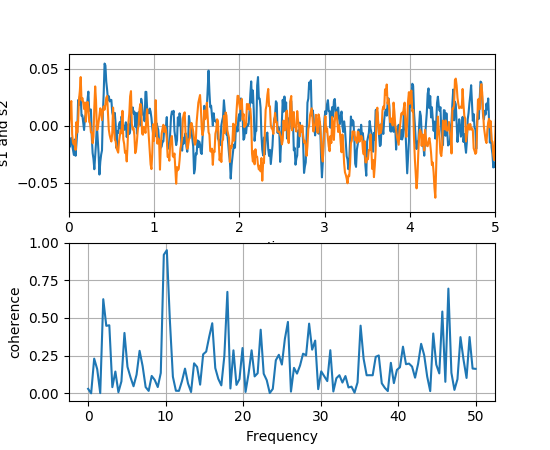
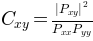| Parameters: | Fs : scalar
The sampling frequency (samples per time unit). It is used
to calculate the Fourier frequencies, freqs, in cycles per time
unit. The default value is 2.
window : callable or ndarray
A function or a vector of length NFFT. To create window
vectors see window_hanning(), window_none(),
numpy.blackman(), numpy.hamming(),
numpy.bartlett(), scipy.signal(),
scipy.signal.get_window(), etc. The default is
window_hanning(). If a function is passed as the
argument, it must take a data segment as an argument and
return the windowed version of the segment.
sides : [ ‘default’ | ‘onesided’ | ‘twosided’ ]
Specifies which sides of the spectrum to return. Default gives the
default behavior, which returns one-sided for real data and both
for complex data. ‘onesided’ forces the return of a one-sided
spectrum, while ‘twosided’ forces two-sided.
pad_to : integer
The number of points to which the data segment is padded when
performing the FFT. This can be different from NFFT, which
specifies the number of data points used. While not increasing
the actual resolution of the spectrum (the minimum distance between
resolvable peaks), this can give more points in the plot,
allowing for more detail. This corresponds to the n parameter
in the call to fft(). The default is None, which sets pad_to
equal to NFFT
NFFT : integer
The number of data points used in each block for the FFT.
A power 2 is most efficient. The default value is 256.
This should NOT be used to get zero padding, or the scaling of the
result will be incorrect. Use pad_to for this instead.
detrend : {‘default’, ‘constant’, ‘mean’, ‘linear’, ‘none’} or callable
The function applied to each segment before fft-ing,
designed to remove the mean or linear trend. Unlike in
MATLAB, where the detrend parameter is a vector, in
matplotlib is it a function. The pylab
module defines detrend_none(),
detrend_mean(), and
detrend_linear(), but you can use
a custom function as well. You can also use a string to choose
one of the functions. ‘default’, ‘constant’, and ‘mean’ call
detrend_mean(). ‘linear’ calls
detrend_linear(). ‘none’ calls
detrend_none().
scale_by_freq : boolean, optional
Specifies whether the resulting density values should be scaled
by the scaling frequency, which gives density in units of Hz^-1.
This allows for integration over the returned frequency values.
The default is True for MATLAB compatibility.
noverlap : integer
The number of points of overlap between blocks. The
default value is 0 (no overlap).
Fc : integer
The center frequency of x (defaults to 0), which offsets
the x extents of the plot to reflect the frequency range used
when a signal is acquired and then filtered and downsampled to
baseband.
**kwargs :
Keyword arguments control the Line2D
properties of the coherence plot:
|
|---|