
matplotlib.mlab¶Numerical python functions written for compatability with MATLAB commands with the same names.
cohere()csd()detrend()find()griddata()prctile()prepca()psd()rk4()specgram()Functions that don’t exist in MATLAB, but are useful anyway:
cohere_pairs()rk4()contiguous_regions()cross_from_below()cross_from_above()complex_spectrum()magnitude_spectrum()angle_spectrum()phase_spectrum()detrend_mean()demean()detrend_mean() except for the default axis.detrend_linear()detrend_none()stride_windows()stride_repeat()apply_window()A collection of helper methods for numpyrecord arrays
See misc Examples
rec2txt()rec2csv()csv2rec()rec_append_fields()rec_drop_fields()rec_join()recs_join()rec_groupby()rec_summarize()For the rec viewer functions(e rec2csv), there are a bunch of Format objects you can pass into the functions that will do things like color negative values red, set percent formatting and scaling, etc.
Example usage:
r = csv2rec('somefile.csv', checkrows=0)
formatd = dict(
weight = FormatFloat(2),
change = FormatPercent(2),
cost = FormatThousands(2),
)
rec2excel(r, 'test.xls', formatd=formatd)
rec2csv(r, 'test.csv', formatd=formatd)
scroll = rec2gtk(r, formatd=formatd)
win = gtk.Window()
win.set_size_request(600,800)
win.add(scroll)
win.show_all()
gtk.main()
The following are deprecated; please import directly from numpy (with care–function signatures may differ):
load()save()matplotlib.mlab.FIFOBuffer(*args, **kwargs)¶A FIFO queue to hold incoming x, y data in a rotating buffer using numpy arrays under the hood. It is assumed that you will call asarrays much less frequently than you add data to the queue – otherwise another data structure will be faster.
This can be used to support plots where data is added from a real time feed and the plot object wants to grab data from the buffer and plot it to screen less freqeuently than the incoming.
If you set the dataLim attr to
BBox (eg
matplotlib.Axes.dataLim), the dataLim will be updated as
new data come in.
TODO: add a grow method that will extend nmax
Note
mlab seems like the wrong place for this class.
Deprecated since version 1.3: The FIFOBuffer class was deprecated in version 1.3.
Buffer up to nmax points.
add(x, y)¶Add scalar x and y to the queue.
asarrays()¶Return x and y as arrays; their length will be the len of data added or nmax.
last()¶Get the last x, y or None. None if no data set.
register(func, N)¶Call func every time N events are passed; func signature
is func(fifo).
update_datalim_to_current()¶Update the datalim in the current data in the fifo.
matplotlib.mlab.FormatBool¶Bases: matplotlib.mlab.FormatObj
fromstr(s)¶toval(x)¶matplotlib.mlab.FormatDate(fmt)¶Bases: matplotlib.mlab.FormatObj
fromstr(x)¶toval(x)¶matplotlib.mlab.FormatDatetime(fmt=u'%Y-%m-%d %H:%M:%S')¶Bases: matplotlib.mlab.FormatDate
fromstr(x)¶matplotlib.mlab.FormatFloat(precision=4, scale=1.0)¶Bases: matplotlib.mlab.FormatFormatStr
fromstr(s)¶toval(x)¶matplotlib.mlab.FormatFormatStr(fmt)¶Bases: matplotlib.mlab.FormatObj
tostr(x)¶matplotlib.mlab.FormatInt¶Bases: matplotlib.mlab.FormatObj
fromstr(s)¶tostr(x)¶toval(x)¶matplotlib.mlab.FormatMillions(precision=4)¶Bases: matplotlib.mlab.FormatFloat
matplotlib.mlab.FormatPercent(precision=4)¶Bases: matplotlib.mlab.FormatFloat
matplotlib.mlab.FormatString¶Bases: matplotlib.mlab.FormatObj
tostr(x)¶matplotlib.mlab.FormatThousands(precision=4)¶Bases: matplotlib.mlab.FormatFloat
matplotlib.mlab.GaussianKDE(dataset, bw_method=None)¶Bases: object
Representation of a kernel-density estimate using Gaussian kernels.
Call signature:: kde = GaussianKDE(dataset, bw_method=’silverman’)
| Parameters: | dataset : array_like
bw_method : str, scalar or callable, optional
|
|---|
Attributes
| dataset | ndarray | The dataset with which gaussian_kde was initialized. |
| dim | int | Number of dimensions. |
| num_dp | int | Number of datapoints. |
| factor | float | The bandwidth factor, obtained from kde.covariance_factor, with which
the covariance matrix is multiplied. |
| covariance | ndarray | The covariance matrix of dataset, scaled by the calculated bandwidth
(kde.factor). |
| inv_cov | ndarray | The inverse of covariance. |
Methods
| kde.evaluate(points) | ndarray | Evaluate the estimated pdf on a provided set of points. |
| kde(points) | ndarray | Same as kde.evaluate(points) |
covariance_factor()¶evaluate(points)¶Evaluate the estimated pdf on a set of points.
| Parameters: | points : (# of dimensions, # of points)-array
|
|---|---|
| Returns: | values : (# of points,)-array
|
| Raises: | ValueError : if the dimensionality of the input points is different
|
scotts_factor()¶silverman_factor()¶matplotlib.mlab.PCA(a, standardize=True)¶compute the SVD of a and store data for PCA. Use project to project the data onto a reduced set of dimensions
Inputs:
a: a numobservations x numdims array standardize: True if input data are to be standardized. If False, only centering will be carried out.
Attrs:
a a centered unit sigma version of input a
numrows, numcols: the dimensions of a
mu : a numdims array of means of a. This is the vector that points to the origin of PCA space.
sigma : a numdims array of standard deviation of a
fracs : the proportion of variance of each of the principal components
s : the actual eigenvalues of the decomposition
Wt : the weight vector for projecting a numdims point or array into PCA space
Y : a projected into PCA space
The factor loadings are in the Wt factor, ie the factor loadings for the 1st principal component are given by Wt[0]. This row is also the 1st eigenvector.
center(x)¶center and optionally standardize the data using the mean and sigma from training set a
project(x, minfrac=0.0)¶project x onto the principle axes, dropping any axes where fraction of variance<minfrac
matplotlib.mlab.amap(function, sequence[, sequence, ...]) → array.¶Works like map(), but it returns an array. This is just a
convenient shorthand for numpy.array(map(...)).
matplotlib.mlab.angle_spectrum(x, Fs=None, window=None, pad_to=None, sides=None)¶Compute the angle of the frequency spectrum (wrapped phase spectrum) of x. Data is padded to a length of pad_to and the windowing function window is applied to the signal.
- x: 1-D array or sequence
- Array or sequence containing the data
Keyword arguments:
- Fs: scalar
- The sampling frequency (samples per time unit). It is used to calculate the Fourier frequencies, freqs, in cycles per time unit. The default value is 2.
- window: callable or ndarray
- A function or a vector of length NFFT. To create window vectors see
window_hanning(),window_none(),numpy.blackman(),numpy.hamming(),numpy.bartlett(),scipy.signal(),scipy.signal.get_window(), etc. The default iswindow_hanning(). If a function is passed as the argument, it must take a data segment as an argument and return the windowed version of the segment.- sides: [ ‘default’ | ‘onesided’ | ‘twosided’ ]
- Specifies which sides of the spectrum to return. Default gives the default behavior, which returns one-sided for real data and both for complex data. ‘onesided’ forces the return of a one-sided spectrum, while ‘twosided’ forces two-sided.
Returns the tuple (spectrum, freqs):
- spectrum: 1-D array
- The values for the angle spectrum in radians (real valued)
- freqs: 1-D array
- The frequencies corresponding to the elements in spectrum
See also
complex_spectrum()complex_spectrum().magnitude_spectrum()angle_spectrum() returns the magnitudes of the
corresponding frequencies.phase_spectrum()phase_spectrum() returns the unwrapped version of this
function.specgram()specgram() can return the angle spectrum of segments
within the signal.matplotlib.mlab.apply_window(x, window, axis=0, return_window=None)¶Apply the given window to the given 1D or 2D array along the given axis.
Call signature:
apply_window(x, window, axis=0, return_window=False)
*x*: 1D or 2D array or sequence
Array or sequence containing the data.
*winodw*: function or array.
Either a function to generate a window or an array with length
*x*.shape[*axis*]
*axis*: integer
The axis over which to do the repetition.
Must be 0 or 1. The default is 0
*return_window*: bool
If true, also return the 1D values of the window that was applied
matplotlib.mlab.base_repr(number, base=2, padding=0)¶Return the representation of a number in any given base.
matplotlib.mlab.binary_repr(number, max_length=1025)¶Return the binary representation of the input number as a string.
This is more efficient than using base_repr() with base 2.
Increase the value of max_length for very large numbers. Note that on 32-bit machines, 2**1023 is the largest integer power of 2 which can be converted to a Python float.
matplotlib.mlab.bivariate_normal(X, Y, sigmax=1.0, sigmay=1.0, mux=0.0, muy=0.0, sigmaxy=0.0)¶Bivariate Gaussian distribution for equal shape X, Y.
See bivariate normal at mathworld.
matplotlib.mlab.center_matrix(M, dim=0)¶Return the matrix M with each row having zero mean and unit std.
If dim = 1 operate on columns instead of rows. (dim is opposite to the numpy axis kwarg.)
matplotlib.mlab.cohere(x, y, NFFT=256, Fs=2, detrend=<function detrend_none at 0x7fc4f7fc2c08>, window=<function window_hanning at 0x7fc4f7fc2938>, noverlap=0, pad_to=None, sides=u'default', scale_by_freq=None)¶The coherence between x and y. Coherence is the normalized cross spectral density:
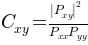
Keyword arguments:
- Fs: scalar
- The sampling frequency (samples per time unit). It is used to calculate the Fourier frequencies, freqs, in cycles per time unit. The default value is 2.
- window: callable or ndarray
- A function or a vector of length NFFT. To create window vectors see
window_hanning(),window_none(),numpy.blackman(),numpy.hamming(),numpy.bartlett(),scipy.signal(),scipy.signal.get_window(), etc. The default iswindow_hanning(). If a function is passed as the argument, it must take a data segment as an argument and return the windowed version of the segment.- sides: [ ‘default’ | ‘onesided’ | ‘twosided’ ]
- Specifies which sides of the spectrum to return. Default gives the default behavior, which returns one-sided for real data and both for complex data. ‘onesided’ forces the return of a one-sided spectrum, while ‘twosided’ forces two-sided.
callable
The function applied to each segment before fft-ing,
designed to remove the mean or linear trend. Unlike in
MATLAB, where the detrend parameter is a vector, in
matplotlib is it a function. The pylab
module defines detrend_none(),
detrend_mean(), and
detrend_linear(), but you can use
a custom function as well. You can also use a string to choose
one of the functions. ‘default’, ‘constant’, and ‘mean’ call
detrend_mean(). ‘linear’ calls
detrend_linear(). ‘none’ calls
detrend_none().
Specifies whether the resulting density values should be scaled by the scaling frequency, which gives density in units of Hz^-1. This allows for integration over the returned frequency values. The default is True for MATLAB compatibility.
The return value is the tuple (Cxy, f), where f are the frequencies of the coherence vector. For cohere, scaling the individual densities by the sampling frequency has no effect, since the factors cancel out.
matplotlib.mlab.cohere_pairs(X, ij, NFFT=256, Fs=2, detrend=<function detrend_none at 0x7fc4f7fc2c08>, window=<function window_hanning at 0x7fc4f7fc2938>, noverlap=0, preferSpeedOverMemory=True, progressCallback=<function donothing_callback at 0x7fc4f7f61488>, returnPxx=False)¶Call signature:
Cxy, Phase, freqs = cohere_pairs( X, ij, ...)
Compute the coherence and phase for all pairs ij, in X.
X is a numSamples * numCols array
ij is a list of tuples. Each tuple is a pair of indexes into the columns of X for which you want to compute coherence. For example, if X has 64 columns, and you want to compute all nonredundant pairs, define ij as:
ij = []
for i in range(64):
for j in range(i+1,64):
ij.append( (i,j) )
preferSpeedOverMemory is an optional bool. Defaults to true. If
False, limits the caching by only making one, rather than two,
complex cache arrays. This is useful if memory becomes critical.
Even when preferSpeedOverMemory is False, cohere_pairs()
will still give significant performace gains over calling
cohere() for each pair, and will use subtantially less
memory than if preferSpeedOverMemory is True. In my tests with
a 43000,64 array over all nonredundant pairs,
preferSpeedOverMemory = True delivered a 33% performance boost
on a 1.7GHZ Athlon with 512MB RAM compared with
preferSpeedOverMemory = False. But both solutions were more
than 10x faster than naively crunching all possible pairs through
cohere().
Returns:
(Cxy, Phase, freqs)
where:
Cxy: dictionary of (i, j) tuples -> coherence vector for that pair. I.e.,
Cxy[(i,j) = cohere(X[:,i], X[:,j]). Number of dictionary keys islen(ij).Phase: dictionary of phases of the cross spectral density at each frequency for each pair. Keys are (i, j).
- freqs: vector of frequencies, equal in length to either the
coherence or phase vectors for any (i, j) key.
e.g., to make a coherence Bode plot:
subplot(211)
plot( freqs, Cxy[(12,19)])
subplot(212)
plot( freqs, Phase[(12,19)])
For a large number of pairs, cohere_pairs() can be much more
efficient than just calling cohere() for each pair, because
it caches most of the intensive computations. If 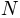 is the
number of pairs, this function is
is the
number of pairs, this function is 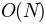 for most of the
heavy lifting, whereas calling cohere for each pair is
for most of the
heavy lifting, whereas calling cohere for each pair is
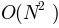 . However, because of the caching, it is also more
memory intensive, making 2 additional complex arrays with
approximately the same number of elements as X.
. However, because of the caching, it is also more
memory intensive, making 2 additional complex arrays with
approximately the same number of elements as X.
See test/cohere_pairs_test.py in the src tree for an
example script that shows that this cohere_pairs() and
cohere() give the same results for a given pair.
See also
psd()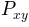 ,
, 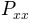 and
and  .
.matplotlib.mlab.complex_spectrum(x, Fs=None, window=None, pad_to=None, sides=None)¶Compute the complex-valued frequency spectrum of x. Data is padded to a length of pad_to and the windowing function window is applied to the signal.
- x: 1-D array or sequence
- Array or sequence containing the data
Keyword arguments:
- Fs: scalar
- The sampling frequency (samples per time unit). It is used to calculate the Fourier frequencies, freqs, in cycles per time unit. The default value is 2.
- window: callable or ndarray
- A function or a vector of length NFFT. To create window vectors see
window_hanning(),window_none(),numpy.blackman(),numpy.hamming(),numpy.bartlett(),scipy.signal(),scipy.signal.get_window(), etc. The default iswindow_hanning(). If a function is passed as the argument, it must take a data segment as an argument and return the windowed version of the segment.- sides: [ ‘default’ | ‘onesided’ | ‘twosided’ ]
- Specifies which sides of the spectrum to return. Default gives the default behavior, which returns one-sided for real data and both for complex data. ‘onesided’ forces the return of a one-sided spectrum, while ‘twosided’ forces two-sided.
Returns the tuple (spectrum, freqs):
- spectrum: 1-D array
- The values for the complex spectrum (complex valued)
- freqs: 1-D array
- The frequencies corresponding to the elements in spectrum
See also
magnitude_spectrum()magnitude_spectrum() returns the absolute value of this
function.angle_spectrum()angle_spectrum() returns the angle of this
function.phase_spectrum()phase_spectrum() returns the phase (unwrapped angle) of this
function.specgram()specgram() can return the complex spectrum of segments
within the signal.matplotlib.mlab.contiguous_regions(mask)¶return a list of (ind0, ind1) such that mask[ind0:ind1].all() is True and we cover all such regions
TODO: this is a pure python implementation which probably has a much faster numpy impl
matplotlib.mlab.cross_from_above(x, threshold)¶return the indices into x where x crosses some threshold from below, eg the i’s where:
x[i-1]>threshold and x[i]<=threshold
See also
matplotlib.mlab.cross_from_below(x, threshold)¶return the indices into x where x crosses some threshold from below, eg the i’s where:
x[i-1]<threshold and x[i]>=threshold
Example code:
import matplotlib.pyplot as plt
t = np.arange(0.0, 2.0, 0.1)
s = np.sin(2*np.pi*t)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(t, s, '-o')
ax.axhline(0.5)
ax.axhline(-0.5)
ind = cross_from_below(s, 0.5)
ax.vlines(t[ind], -1, 1)
ind = cross_from_above(s, -0.5)
ax.vlines(t[ind], -1, 1)
plt.show()
See also
matplotlib.mlab.csd(x, y, NFFT=None, Fs=None, detrend=None, window=None, noverlap=None, pad_to=None, sides=None, scale_by_freq=None)¶Compute the cross-spectral density.
Call signature:
csd(x, y, NFFT=256, Fs=2, detrend=mlab.detrend_none,
window=mlab.window_hanning, noverlap=0, pad_to=None,
sides='default', scale_by_freq=None)
The cross spectral density 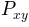 by Welch’s average
periodogram method. The vectors x and y are divided into
NFFT length segments. Each segment is detrended by function
detrend and windowed by function window. noverlap gives
the length of the overlap between segments. The product of
the direct FFTs of x and y are averaged over each segment
to compute
by Welch’s average
periodogram method. The vectors x and y are divided into
NFFT length segments. Each segment is detrended by function
detrend and windowed by function window. noverlap gives
the length of the overlap between segments. The product of
the direct FFTs of x and y are averaged over each segment
to compute 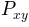 , with a scaling to correct for power
loss due to windowing.
, with a scaling to correct for power
loss due to windowing.
If len(x) < NFFT or len(y) < NFFT, they will be zero padded to NFFT.
- x, y: 1-D arrays or sequences
- Arrays or sequences containing the data
Keyword arguments:
- Fs: scalar
- The sampling frequency (samples per time unit). It is used to calculate the Fourier frequencies, freqs, in cycles per time unit. The default value is 2.
- window: callable or ndarray
- A function or a vector of length NFFT. To create window vectors see
window_hanning(),window_none(),numpy.blackman(),numpy.hamming(),numpy.bartlett(),scipy.signal(),scipy.signal.get_window(), etc. The default iswindow_hanning(). If a function is passed as the argument, it must take a data segment as an argument and return the windowed version of the segment.- sides: [ ‘default’ | ‘onesided’ | ‘twosided’ ]
- Specifies which sides of the spectrum to return. Default gives the default behavior, which returns one-sided for real data and both for complex data. ‘onesided’ forces the return of a one-sided spectrum, while ‘twosided’ forces two-sided.
callable
The function applied to each segment before fft-ing,
designed to remove the mean or linear trend. Unlike in
MATLAB, where the detrend parameter is a vector, in
matplotlib is it a function. The pylab
module defines detrend_none(),
detrend_mean(), and
detrend_linear(), but you can use
a custom function as well. You can also use a string to choose
one of the functions. ‘default’, ‘constant’, and ‘mean’ call
detrend_mean(). ‘linear’ calls
detrend_linear(). ‘none’ calls
detrend_none().
Specifies whether the resulting density values should be scaled by the scaling frequency, which gives density in units of Hz^-1. This allows for integration over the returned frequency values. The default is True for MATLAB compatibility.
Returns the tuple (Pxy, freqs):
- Pxy: 1-D array
- The values for the cross spectrum
P_{xy}before scaling (real valued)- freqs: 1-D array
- The frequencies corresponding to the elements in Pxy
matplotlib.mlab.csv2rec(fname, comments=u'#', skiprows=0, checkrows=0, delimiter=u', ', converterd=None, names=None, missing=u'', missingd=None, use_mrecords=False, dayfirst=False, yearfirst=False)¶Load data from comma/space/tab delimited file in fname into a numpy record array and return the record array.
If names is None, a header row is required to automatically assign the recarray names. The headers will be lower cased, spaces will be converted to underscores, and illegal attribute name characters removed. If names is not None, it is a sequence of names to use for the column names. In this case, it is assumed there is no header row.
fname: can be a filename or a file handle. Support for gzipped files is automatic, if the filename ends in ‘.gz’
comments: the character used to indicate the start of a comment in the file, or None to switch off the removal of comments
skiprows: is the number of rows from the top to skip
checkrows: is the number of rows to check to validate the column data type. When set to zero all rows are validated.
converterd: if not None, is a dictionary mapping column number or munged column name to a converter function.
names: if not None, is a list of header names. In this case, no header will be read from the file
missingd is a dictionary mapping munged column names to field values which signify that the field does not contain actual data and should be masked, e.g., ‘0000-00-00’ or ‘unused’
missing: a string whose value signals a missing field regardless of the column it appears in
use_mrecords: if True, return an mrecords.fromrecords record array if any of the data are missing
dayfirst: default is False so that MM-DD-YY has precedence over DD-MM-YY. See http://labix.org/python-dateutil#head-b95ce2094d189a89f80f5ae52a05b4ab7b41af47 for further information.
yearfirst: default is False so that MM-DD-YY has precedence over YY-MM-DD. See http://labix.org/python-dateutil#head-b95ce2094d189a89f80f5ae52a05b4ab7b41af47 for further information.
If no rows are found, None is returned – see examples/loadrec.py
matplotlib.mlab.csvformat_factory(format)¶matplotlib.mlab.demean(x, axis=0)¶Return x minus its mean along the specified axis.
Call signature:
demean(x, axis=0)
*x*: array or sequence
Array or sequence containing the data
Can have any dimensionality
*axis*: integer
The axis along which to take the mean. See numpy.mean for a
description of this argument.
See also
delinear()
denone()delinear() and denone() are other detrend algorithms.detrend_mean()detrend_mean() except
for the default axis.matplotlib.mlab.detrend(x, key=None, axis=None)¶Return x with its trend removed.
Call signature:
detrend(x, key='mean')
*x*: array or sequence
Array or sequence containing the data.
*key*: [ 'default' | 'constant' | 'mean' | 'linear' | 'none'] or function
Specifies the detrend algorithm to use. 'default' is 'mean',
which is the same as :func:`detrend_mean`. 'constant' is the same.
'linear' is the same as :func:`detrend_linear`. 'none' is the same
as :func:`detrend_none`. The default is 'mean'. See the
corresponding functions for more details regarding the algorithms.
Can also be a function that carries out the detrend operation.
*axis*: integer
The axis along which to do the detrending.
See also
detrend_mean()detrend_mean() implements the ‘mean’ algorithm.detrend_linear()detrend_linear() implements the ‘linear’ algorithm.detrend_none()detrend_none() implements the ‘none’ algorithm.matplotlib.mlab.detrend_linear(y)¶Return x minus best fit line; ‘linear’ detrending.
Call signature:
detrend_linear(y)
*y*: 0-D or 1-D array or sequence
Array or sequence containing the data
*axis*: integer
The axis along which to take the mean. See numpy.mean for a
description of this argument.
See also
delinear()delinear() except
for the default axis.detrend_none()detrend_mean() and detrend_none() are other
detrend algorithms.detrend()detrend() is a wrapper around all the detrend algorithms.matplotlib.mlab.detrend_mean(x, axis=None)¶Return x minus the mean(x).
Call signature:
detrend_mean(x, axis=None)
*x*: array or sequence
Array or sequence containing the data
Can have any dimensionality
*axis*: integer
The axis along which to take the mean. See numpy.mean for a
description of this argument.
See also
detrend_none()detrend_linear() and detrend_none() are other
detrend algorithms.detrend()detrend() is a wrapper around all the detrend algorithms.matplotlib.mlab.detrend_none(x, axis=None)¶Return x: no detrending.
Call signature:
detrend_none(x, axis=None)
*x*: any object
An object containing the data
*axis*: integer
This parameter is ignored.
It is included for compatibility with detrend_mean
See also
denone()denone() except
for the default axis, which has no effect.detrend_linear()detrend_mean() and detrend_linear() are other
detrend algorithms.detrend()detrend() is a wrapper around all the detrend algorithms.matplotlib.mlab.dist(x, y)¶Return the distance between two points.
matplotlib.mlab.dist_point_to_segment(p, s0, s1)¶Get the distance of a point to a segment.
p, s0, s1 are xy sequences
This algorithm from http://softsurfer.com/Archive/algorithm_0102/algorithm_0102.htm#Distance%20to%20Ray%20or%20Segment
matplotlib.mlab.distances_along_curve(X)¶Computes the distance between a set of successive points in N dimensions.
Where X is an M x N array or matrix. The distances between successive rows is computed. Distance is the standard Euclidean distance.
matplotlib.mlab.donothing_callback(*args)¶matplotlib.mlab.entropy(y, bins)¶Return the entropy of the data in y in units of nat.
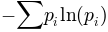
where 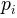 is the probability of observing y in the
is the probability of observing y in the
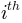 bin of bins. bins can be a number of bins or a
range of bins; see
bin of bins. bins can be a number of bins or a
range of bins; see numpy.histogram().
Compare S with analytic calculation for a Gaussian:
x = mu + sigma * randn(200000)
Sanalytic = 0.5 * ( 1.0 + log(2*pi*sigma**2.0) )
matplotlib.mlab.exp_safe(x)¶Compute exponentials which safely underflow to zero.
Slow, but convenient to use. Note that numpy provides proper floating point exception handling with access to the underlying hardware.
matplotlib.mlab.fftsurr(x, detrend=<function detrend_none at 0x7fc4f7fc2c08>, window=<function window_none at 0x7fc4f7fc29b0>)¶Compute an FFT phase randomized surrogate of x.
matplotlib.mlab.find(condition)¶Return the indices where ravel(condition) is true
matplotlib.mlab.frange([start, ]stop[, step, keywords]) → array of floats¶Return a numpy ndarray containing a progression of floats. Similar to
numpy.arange(), but defaults to a closed interval.
frange(x0, x1) returns [x0, x0+1, x0+2, ..., x1]; start
defaults to 0, and the endpoint is included. This behavior is
different from that of range() and
numpy.arange(). This is deliberate, since frange()
will probably be more useful for generating lists of points for
function evaluation, and endpoints are often desired in this
use. The usual behavior of range() can be obtained by
setting the keyword closed = 0, in this case, frange()
basically becomes :func:numpy.arange`.
When step is given, it specifies the increment (or decrement). All arguments can be floating point numbers.
frange(x0,x1,d) returns [x0,x0+d,x0+2d,...,xfin] where
xfin <= x1.
frange() can also be called with the keyword npts. This
sets the number of points the list should contain (and overrides
the value step might have been given). numpy.arange()
doesn’t offer this option.
Examples:
>>> frange(3)
array([ 0., 1., 2., 3.])
>>> frange(3,closed=0)
array([ 0., 1., 2.])
>>> frange(1,6,2)
array([1, 3, 5]) or 1,3,5,7, depending on floating point vagueries
>>> frange(1,6.5,npts=5)
array([ 1. , 2.375, 3.75 , 5.125, 6.5 ])
matplotlib.mlab.get_formatd(r, formatd=None)¶build a formatd guaranteed to have a key for every dtype name
matplotlib.mlab.get_sparse_matrix(M, N, frac=0.1)¶Return a M x N sparse matrix with frac elements randomly filled.
matplotlib.mlab.get_xyz_where(Z, Cond)¶Z and Cond are M x N matrices. Z are data and Cond is a boolean matrix where some condition is satisfied. Return value is (x, y, z) where x and y are the indices into Z and z are the values of Z at those indices. x, y, and z are 1D arrays.
matplotlib.mlab.griddata(x, y, z, xi, yi, interp=u'nn')¶Interpolates from a nonuniformly spaced grid to some other grid.
Fits a surface of the form z = f(x, y) to the data in the
(usually) nonuniformly spaced vectors (x, y, z), then
interpolates this surface at the points specified by
(xi, yi) to produce zi.
| Parameters: | x, y, z : 1d array_like
xi, yi : 1d or 2d array_like
interp : string key from {‘nn’, ‘linear’}
|
|---|---|
| Returns: | 2d float array :
|
Notes
If interp is ‘nn’ (the default), uses natural neighbor
interpolation based on Delaunay triangulation. This option is
only available if the mpl_toolkits.natgrid module is installed.
This can be downloaded from https://github.com/matplotlib/natgrid.
The (xi, yi) grid must be regular and monotonically increasing
in this case.
If interp is ‘linear’, linear interpolation is used via
matplotlib.tri.LinearTriInterpolator.
Instead of using griddata, more flexible functionality and other
interpolation options are available using a
matplotlib.tri.Triangulation and a matplotlib.tri.TriInterpolator.
matplotlib.mlab.identity(n, rank=2, dtype=u'l', typecode=None)¶Returns the identity matrix of shape (n, n, ..., n) (rank r).
For ranks higher than 2, this object is simply a multi-index Kronecker delta:
/ 1 if i0=i1=...=iR,
id[i0,i1,...,iR] = -|
\ 0 otherwise.
Optionally a dtype (or typecode) may be given (it defaults to ‘l’).
Since rank defaults to 2, this function behaves in the default case (when
only n is given) like numpy.identity(n) – but surprisingly, it is
much faster.
matplotlib.mlab.inside_poly(points, verts)¶points is a sequence of x, y points. verts is a sequence of x, y vertices of a polygon.
Return value is a sequence of indices into points for the points that are inside the polygon.
matplotlib.mlab.is_closed_polygon(X)¶Tests whether first and last object in a sequence are the same. These are presumably coordinates on a polygonal curve, in which case this function tests if that curve is closed.
matplotlib.mlab.ispower2(n)¶Returns the log base 2 of n if n is a power of 2, zero otherwise.
Note the potential ambiguity if n == 1: 2**0 == 1, interpret accordingly.
matplotlib.mlab.isvector(X)¶Like the MATLAB function with the same name, returns True if the supplied numpy array or matrix X looks like a vector, meaning it has a one non-singleton axis (i.e., it can have multiple axes, but all must have length 1, except for one of them).
If you just want to see if the array has 1 axis, use X.ndim == 1.
matplotlib.mlab.l1norm(a)¶Return the l1 norm of a, flattened out.
Implemented as a separate function (not a call to norm() for speed).
matplotlib.mlab.l2norm(a)¶Return the l2 norm of a, flattened out.
Implemented as a separate function (not a call to norm() for speed).
matplotlib.mlab.less_simple_linear_interpolation(x, y, xi, extrap=False)¶This function provides simple (but somewhat less so than
cbook.simple_linear_interpolation()) linear interpolation.
simple_linear_interpolation() will give a list of point
between a start and an end, while this does true linear
interpolation at an arbitrary set of points.
This is very inefficient linear interpolation meant to be used only for a small number of points in relatively non-intensive use cases. For real linear interpolation, use scipy.
matplotlib.mlab.log2(x, ln2=0.6931471805599453)¶Return the log(x) in base 2.
This is a _slow_ function but which is guaranteed to return the correct integer value if the input is an integer exact power of 2.
matplotlib.mlab.logspace(xmin, xmax, N)¶Return N values logarithmically spaced between xmin and xmax.
Call signature:
logspace(xmin, xmax, N)
matplotlib.mlab.longest_contiguous_ones(x)¶Return the indices of the longest stretch of contiguous ones in x, assuming x is a vector of zeros and ones. If there are two equally long stretches, pick the first.
matplotlib.mlab.longest_ones(x)¶alias for longest_contiguous_ones
matplotlib.mlab.magnitude_spectrum(x, Fs=None, window=None, pad_to=None, sides=None)¶Compute the magnitude (absolute value) of the frequency spectrum of x. Data is padded to a length of pad_to and the windowing function window is applied to the signal.
- x: 1-D array or sequence
- Array or sequence containing the data
Keyword arguments:
- Fs: scalar
- The sampling frequency (samples per time unit). It is used to calculate the Fourier frequencies, freqs, in cycles per time unit. The default value is 2.
- window: callable or ndarray
- A function or a vector of length NFFT. To create window vectors see
window_hanning(),window_none(),numpy.blackman(),numpy.hamming(),numpy.bartlett(),scipy.signal(),scipy.signal.get_window(), etc. The default iswindow_hanning(). If a function is passed as the argument, it must take a data segment as an argument and return the windowed version of the segment.- sides: [ ‘default’ | ‘onesided’ | ‘twosided’ ]
- Specifies which sides of the spectrum to return. Default gives the default behavior, which returns one-sided for real data and both for complex data. ‘onesided’ forces the return of a one-sided spectrum, while ‘twosided’ forces two-sided.
Returns the tuple (spectrum, freqs):
- spectrum: 1-D array
- The values for the magnitude spectrum (real valued)
- freqs: 1-D array
- The frequencies corresponding to the elements in spectrum
See also
psd()psd() returns the power spectral density.complex_spectrum()complex_spectrum().angle_spectrum()angle_spectrum() returns the angles of the corresponding
frequencies.phase_spectrum()phase_spectrum() returns the phase (unwrapped angle) of the
corresponding frequencies.specgram()specgram() can return the magnitude spectrum of segments
within the signal.matplotlib.mlab.movavg(x, n)¶Compute the len(n) moving average of x.
matplotlib.mlab.norm_flat(a, p=2)¶norm(a,p=2) -> l-p norm of a.flat
Return the l-p norm of a, considered as a flat array. This is NOT a true matrix norm, since arrays of arbitrary rank are always flattened.
p can be a number or the string ‘Infinity’ to get the L-infinity norm.
matplotlib.mlab.normpdf(x, *args)¶Return the normal pdf evaluated at x; args provides mu, sigma
matplotlib.mlab.offset_line(y, yerr)¶Offsets an array y by +/- an error and returns a tuple (y - err, y + err).
The error term can be:
A scalar. In this case, the returned tuple is obvious.
A vector of the same length as y. The quantities y +/- err are computed component-wise.
A tuple of length 2. In this case, yerr[0] is the error below y and yerr[1] is error above y. For example:
from pylab import *
x = linspace(0, 2*pi, num=100, endpoint=True)
y = sin(x)
y_minus, y_plus = mlab.offset_line(y, 0.1)
plot(x, y)
fill_between(x, ym, y2=yp)
show()
matplotlib.mlab.path_length(X)¶Computes the distance travelled along a polygonal curve in N dimensions.
Where X is an M x N array or matrix. Returns an array of length M consisting of the distance along the curve at each point (i.e., the rows of X).
matplotlib.mlab.phase_spectrum(x, Fs=None, window=None, pad_to=None, sides=None)¶Compute the phase of the frequency spectrum (unwrapped angle spectrum) of x. Data is padded to a length of pad_to and the windowing function window is applied to the signal.
- x: 1-D array or sequence
- Array or sequence containing the data
Keyword arguments:
- Fs: scalar
- The sampling frequency (samples per time unit). It is used to calculate the Fourier frequencies, freqs, in cycles per time unit. The default value is 2.
- window: callable or ndarray
- A function or a vector of length NFFT. To create window vectors see
window_hanning(),window_none(),numpy.blackman(),numpy.hamming(),numpy.bartlett(),scipy.signal(),scipy.signal.get_window(), etc. The default iswindow_hanning(). If a function is passed as the argument, it must take a data segment as an argument and return the windowed version of the segment.- sides: [ ‘default’ | ‘onesided’ | ‘twosided’ ]
- Specifies which sides of the spectrum to return. Default gives the default behavior, which returns one-sided for real data and both for complex data. ‘onesided’ forces the return of a one-sided spectrum, while ‘twosided’ forces two-sided.
Returns the tuple (spectrum, freqs):
- spectrum: 1-D array
- The values for the phase spectrum in radians (real valued)
- freqs: 1-D array
- The frequencies corresponding to the elements in spectrum
See also
complex_spectrum()complex_spectrum().magnitude_spectrum()magnitude_spectrum() returns the magnitudes of the
corresponding frequencies.angle_spectrum()angle_spectrum() returns the wrapped version of this
function.specgram()specgram() can return the phase spectrum of segments
within the signal.matplotlib.mlab.poly_below(xmin, xs, ys)¶Given a sequence of xs and ys, return the vertices of a polygon that has a horizontal base at xmin and an upper bound at the ys. xmin is a scalar.
Intended for use with matplotlib.axes.Axes.fill(), eg:
xv, yv = poly_below(0, x, y)
ax.fill(xv, yv)
matplotlib.mlab.poly_between(x, ylower, yupper)¶Given a sequence of x, ylower and yupper, return the polygon that fills the regions between them. ylower or yupper can be scalar or iterable. If they are iterable, they must be equal in length to x.
Return value is x, y arrays for use with
matplotlib.axes.Axes.fill().
matplotlib.mlab.prctile(x, p=(0.0, 25.0, 50.0, 75.0, 100.0))¶Return the percentiles of x. p can either be a sequence of percentile values or a scalar. If p is a sequence, the ith element of the return sequence is the p*(i)-th percentile of *x. If p is a scalar, the largest value of x less than or equal to the p percentage point in the sequence is returned.
matplotlib.mlab.prctile_rank(x, p)¶Return the rank for each element in x, return the rank 0..len(p). e.g., if p = (25, 50, 75), the return value will be a len(x) array with values in [0,1,2,3] where 0 indicates the value is less than the 25th percentile, 1 indicates the value is >= the 25th and < 50th percentile, ... and 3 indicates the value is above the 75th percentile cutoff.
p is either an array of percentiles in [0..100] or a scalar which indicates how many quantiles of data you want ranked.
matplotlib.mlab.prepca(P, frac=0)¶Warning
This function is deprecated – please see class PCA instead
Compute the principal components of P. P is a (numVars, numObs) array. frac is the minimum fraction of variance that a component must contain to be included.
Return value is a tuple of the form (Pcomponents, Trans, fracVar) where:
Pcomponents : a (numVars, numObs) array
- Trans : the weights matrix, ie, Pcomponents = Trans *
P
- fracVar : the fraction of the variance accounted for by each
component returned
A similar function of the same name was in the MATLAB R13 Neural Network Toolbox but is not found in later versions; its successor seems to be called “processpcs”.
matplotlib.mlab.psd(x, NFFT=None, Fs=None, detrend=None, window=None, noverlap=None, pad_to=None, sides=None, scale_by_freq=None)¶Compute the power spectral density.
Call signature:
psd(x, NFFT=256, Fs=2, detrend=mlab.detrend_none,
window=mlab.window_hanning, noverlap=0, pad_to=None,
sides='default', scale_by_freq=None)
The power spectral density 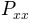 by Welch’s average
periodogram method. The vector x is divided into NFFT length
segments. Each segment is detrended by function detrend and
windowed by function window. noverlap gives the length of
the overlap between segments. The
by Welch’s average
periodogram method. The vector x is divided into NFFT length
segments. Each segment is detrended by function detrend and
windowed by function window. noverlap gives the length of
the overlap between segments. The 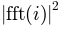 of each segment
of each segment 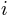 are averaged to compute
are averaged to compute 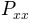 .
.
If len(x) < NFFT, it will be zero padded to NFFT.
- x: 1-D array or sequence
- Array or sequence containing the data
Keyword arguments:
- Fs: scalar
- The sampling frequency (samples per time unit). It is used to calculate the Fourier frequencies, freqs, in cycles per time unit. The default value is 2.
- window: callable or ndarray
- A function or a vector of length NFFT. To create window vectors see
window_hanning(),window_none(),numpy.blackman(),numpy.hamming(),numpy.bartlett(),scipy.signal(),scipy.signal.get_window(), etc. The default iswindow_hanning(). If a function is passed as the argument, it must take a data segment as an argument and return the windowed version of the segment.- sides: [ ‘default’ | ‘onesided’ | ‘twosided’ ]
- Specifies which sides of the spectrum to return. Default gives the default behavior, which returns one-sided for real data and both for complex data. ‘onesided’ forces the return of a one-sided spectrum, while ‘twosided’ forces two-sided.
callable
The function applied to each segment before fft-ing,
designed to remove the mean or linear trend. Unlike in
MATLAB, where the detrend parameter is a vector, in
matplotlib is it a function. The pylab
module defines detrend_none(),
detrend_mean(), and
detrend_linear(), but you can use
a custom function as well. You can also use a string to choose
one of the functions. ‘default’, ‘constant’, and ‘mean’ call
detrend_mean(). ‘linear’ calls
detrend_linear(). ‘none’ calls
detrend_none().
Specifies whether the resulting density values should be scaled by the scaling frequency, which gives density in units of Hz^-1. This allows for integration over the returned frequency values. The default is True for MATLAB compatibility.
noverlap: integer The number of points of overlap between segments. The default value is 0 (no overlap).
Returns the tuple (Pxx, freqs).
- Pxx: 1-D array
- The values for the power spectrum
P_{xx}(real valued)- freqs: 1-D array
- The frequencies corresponding to the elements in Pxx
Refs:
Bendat & Piersol – Random Data: Analysis and Measurement Procedures, John Wiley & Sons (1986)
See also
specgram()specgram() differs in the default overlap; in not returning
the mean of the segment periodograms; and in returning the
times of the segments.magnitude_spectrum()magnitude_spectrum() returns the magnitude spectrum.csd()csd() returns the spectral density between two signals.matplotlib.mlab.quad2cubic(q0x, q0y, q1x, q1y, q2x, q2y)¶Converts a quadratic Bezier curve to a cubic approximation.
The inputs are the x and y coordinates of the three control points of a quadratic curve, and the output is a tuple of x and y coordinates of the four control points of the cubic curve.
matplotlib.mlab.rec2csv(r, fname, delimiter=u', ', formatd=None, missing=u'', missingd=None, withheader=True)¶Save the data from numpy recarray r into a comma-/space-/tab-delimited file. The record array dtype names will be used for column headers.
for formatd type FormatFloat, we override the precision to store full precision floats in the CSV file
See also
csv2rec()matplotlib.mlab.rec2txt(r, header=None, padding=3, precision=3, fields=None)¶Returns a textual representation of a record array.
r: numpy recarray
header: list of column headers
padding: space between each column
fields : if not None, a list of field names to print. fields can be a list of strings like [‘field1’, ‘field2’] or a single comma separated string like ‘field1,field2’
Example:
precision=[0,2,3]
Output:
ID Price Return
ABC 12.54 0.234
XYZ 6.32 -0.076
matplotlib.mlab.rec_append_fields(rec, names, arrs, dtypes=None)¶Return a new record array with field names populated with data from arrays in arrs. If appending a single field, then names, arrs and dtypes do not have to be lists. They can just be the values themselves.
matplotlib.mlab.rec_drop_fields(rec, names)¶Return a new numpy record array with fields in names dropped.
matplotlib.mlab.rec_groupby(r, groupby, stats)¶r is a numpy record array
groupby is a sequence of record array attribute names that together form the grouping key. eg (‘date’, ‘productcode’)
stats is a sequence of (attr, func, outname) tuples which
will call x = func(attr) and assign x to the record array
output with attribute outname. For example:
stats = ( ('sales', len, 'numsales'), ('sales', np.mean, 'avgsale') )
Return record array has dtype names for each attribute name in the the groupby argument, with the associated group values, and for each outname name in the stats argument, with the associated stat summary output.
matplotlib.mlab.rec_join(key, r1, r2, jointype=u'inner', defaults=None, r1postfix=u'1', r2postfix=u'2')¶Join record arrays r1 and r2 on key; key is a tuple of field names – if key is a string it is assumed to be a single attribute name. If r1 and r2 have equal values on all the keys in the key tuple, then their fields will be merged into a new record array containing the intersection of the fields of r1 and r2.
r1 (also r2) must not have any duplicate keys.
The jointype keyword can be ‘inner’, ‘outer’, ‘leftouter’. To do a rightouter join just reverse r1 and r2.
The defaults keyword is a dictionary filled with
{column_name:default_value} pairs.
The keywords r1postfix and r2postfix are postfixed to column names (other than keys) that are both in r1 and r2.
matplotlib.mlab.rec_keep_fields(rec, names)¶Return a new numpy record array with only fields listed in names
matplotlib.mlab.rec_summarize(r, summaryfuncs)¶r is a numpy record array
summaryfuncs is a list of (attr, func, outname) tuples which will apply func to the the array r*[attr] and assign the output to a new attribute name *outname. The returned record array is identical to r, with extra arrays for each element in summaryfuncs.
matplotlib.mlab.recs_join(key, name, recs, jointype=u'outer', missing=0.0, postfixes=None)¶Join a sequence of record arrays on single column key.
This function only joins a single column of the multiple record arrays
returns a record array with columns [rowkey, name0, name1, ... namen-1]. or if postfixes [PF0, PF1, ..., PFN-1] are supplied, [rowkey, namePF0, namePF1, ... namePFN-1].
Example:
r = recs_join("date", "close", recs=[r0, r1], missing=0.)
matplotlib.mlab.rk4(derivs, y0, t)¶Integrate 1D or ND system of ODEs using 4-th order Runge-Kutta.
This is a toy implementation which may be useful if you find
yourself stranded on a system w/o scipy. Otherwise use
scipy.integrate().
dy = derivs(yi, ti)Example 1
## 2D system
def derivs6(x,t):
d1 = x[0] + 2*x[1]
d2 = -3*x[0] + 4*x[1]
return (d1, d2)
dt = 0.0005
t = arange(0.0, 2.0, dt)
y0 = (1,2)
yout = rk4(derivs6, y0, t)
Example 2:
## 1D system
alpha = 2
def derivs(x,t):
return -alpha*x + exp(-t)
y0 = 1
yout = rk4(derivs, y0, t)
If you have access to scipy, you should probably be using the scipy.integrate tools rather than this function.
matplotlib.mlab.rms_flat(a)¶Return the root mean square of all the elements of a, flattened out.
matplotlib.mlab.safe_isinf(x)¶numpy.isinf() for arbitrary types
matplotlib.mlab.safe_isnan(x)¶numpy.isnan() for arbitrary types
matplotlib.mlab.segments_intersect(s1, s2)¶Return True if s1 and s2 intersect. s1 and s2 are defined as:
s1: (x1, y1), (x2, y2)
s2: (x3, y3), (x4, y4)
matplotlib.mlab.slopes(x, y)¶slopes() calculates the slope y‘(x)
The slope is estimated using the slope obtained from that of a parabola through any three consecutive points.
This method should be superior to that described in the appendix of A CONSISTENTLY WELL BEHAVED METHOD OF INTERPOLATION by Russel W. Stineman (Creative Computing July 1980) in at least one aspect:
Circles for interpolation demand a known aspect ratio between x- and y-values. For many functions, however, the abscissa are given in different dimensions, so an aspect ratio is completely arbitrary.
The parabola method gives very similar results to the circle method for most regular cases but behaves much better in special cases.
Norbert Nemec, Institute of Theoretical Physics, University or Regensburg, April 2006 Norbert.Nemec at physik.uni-regensburg.de
(inspired by a original implementation by Halldor Bjornsson, Icelandic Meteorological Office, March 2006 halldor at vedur.is)
matplotlib.mlab.specgram(x, NFFT=None, Fs=None, detrend=None, window=None, noverlap=None, pad_to=None, sides=None, scale_by_freq=None, mode=None)¶Compute a spectrogram.
Call signature:
specgram(x, NFFT=256, Fs=2,detrend=mlab.detrend_none,
window=mlab.window_hanning, noverlap=128,
cmap=None, xextent=None, pad_to=None, sides='default',
scale_by_freq=None, mode='default')
Compute and plot a spectrogram of data in x. Data are split into NFFT length segments and the spectrum of each section is computed. The windowing function window is applied to each segment, and the amount of overlap of each segment is specified with noverlap.
- x: 1-D array or sequence
- Array or sequence containing the data
Keyword arguments:
- Fs: scalar
- The sampling frequency (samples per time unit). It is used to calculate the Fourier frequencies, freqs, in cycles per time unit. The default value is 2.
- window: callable or ndarray
- A function or a vector of length NFFT. To create window vectors see
window_hanning(),window_none(),numpy.blackman(),numpy.hamming(),numpy.bartlett(),scipy.signal(),scipy.signal.get_window(), etc. The default iswindow_hanning(). If a function is passed as the argument, it must take a data segment as an argument and return the windowed version of the segment.- sides: [ ‘default’ | ‘onesided’ | ‘twosided’ ]
- Specifies which sides of the spectrum to return. Default gives the default behavior, which returns one-sided for real data and both for complex data. ‘onesided’ forces the return of a one-sided spectrum, while ‘twosided’ forces two-sided.
callable
The function applied to each segment before fft-ing,
designed to remove the mean or linear trend. Unlike in
MATLAB, where the detrend parameter is a vector, in
matplotlib is it a function. The pylab
module defines detrend_none(),
detrend_mean(), and
detrend_linear(), but you can use
a custom function as well. You can also use a string to choose
one of the functions. ‘default’, ‘constant’, and ‘mean’ call
detrend_mean(). ‘linear’ calls
detrend_linear(). ‘none’ calls
detrend_none().
Specifies whether the resulting density values should be scaled by the scaling frequency, which gives density in units of Hz^-1. This allows for integration over the returned frequency values. The default is True for MATLAB compatibility.
‘angle’ | ‘phase’ ]
What sort of spectrum to use. Default is ‘psd’. which takes the power spectral density. ‘complex’ returns the complex-valued frequency spectrum. ‘magnitude’ returns the magnitude spectrum. ‘angle’ returns the phase spectrum without unwrapping. ‘phase’ returns the phase spectrum with unwrapping.
Returns the tuple (spectrum, freqs, t):
- spectrum: 2-D array
- columns are the periodograms of successive segments
- freqs: 1-D array
- The frequencies corresponding to the rows in spectrum
- t: 1-D array
- The times corresponding to midpoints of segments (i.e the columns in spectrum).
Note
detrend and scale_by_freq only apply when mode is set to ‘psd’
See also
psd()psd() differs in the default overlap; in returning
the mean of the segment periodograms; and in not returning
times.complex_spectrum()magnitude_spectrum()angle_spectrum()phase_spectrum()matplotlib.mlab.stineman_interp(xi, x, y, yp=None)¶Given data vectors x and y, the slope vector yp and a new
abscissa vector xi, the function stineman_interp() uses
Stineman interpolation to calculate a vector yi corresponding to
xi.
Here’s an example that generates a coarse sine curve, then interpolates over a finer abscissa:
x = linspace(0,2*pi,20); y = sin(x); yp = cos(x)
xi = linspace(0,2*pi,40);
yi = stineman_interp(xi,x,y,yp);
plot(x,y,'o',xi,yi)
The interpolation method is described in the article A CONSISTENTLY WELL BEHAVED METHOD OF INTERPOLATION by Russell W. Stineman. The article appeared in the July 1980 issue of Creative Computing with a note from the editor stating that while they were:
not an academic journal but once in a while something serious and original comes in adding that this was “apparently a real solution” to a well known problem.
For yp = None, the routine automatically determines the slopes
using the slopes() routine.
x is assumed to be sorted in increasing order.
For values xi[j] < x[0] or xi[j] > x[-1], the routine
tries an extrapolation. The relevance of the data obtained from
this, of course, is questionable...
Original implementation by Halldor Bjornsson, Icelandic Meteorolocial Office, March 2006 halldor at vedur.is
Completely reworked and optimized for Python by Norbert Nemec, Institute of Theoretical Physics, University or Regensburg, April 2006 Norbert.Nemec at physik.uni-regensburg.de
matplotlib.mlab.stride_repeat(x, n, axis=0)¶Repeat the values in an array in a memory-efficient manner. Array x is stacked vertically n times.
Warning
It is not safe to write to the output array. Multiple elements may point to the same piece of memory, so modifying one value may change others.
Call signature:
stride_repeat(x, n, axis=0)
*x*: 1D array or sequence
Array or sequence containing the data.
*n*: integer
The number of time to repeat the array.
*axis*: integer
The axis along which the data will run.
matplotlib.mlab.stride_windows(x, n, noverlap=None, axis=0)¶Get all windows of x with length n as a single array, using strides to avoid data duplication.
Warning
It is not safe to write to the output array. Multiple elements may point to the same piece of memory, so modifying one value may change others.
Call signature:
stride_windows(x, n, noverlap=0)
*x*: 1D array or sequence
Array or sequence containing the data.
*n*: integer
The number of data points in each window.
*noverlap*: integer
The overlap between adjacent windows.
Default is 0 (no overlap)
*axis*: integer
The axis along which the windows will run.
matplotlib.mlab.vector_lengths(X, P=2.0, axis=None)¶Finds the length of a set of vectors in n dimensions. This is
like the numpy.norm() function for vectors, but has the ability to
work over a particular axis of the supplied array or matrix.
Computes (sum((x_i)^P))^(1/P) for each {x_i} being the
elements of X along the given axis. If axis is None,
compute over all elements of X.
matplotlib.mlab.window_hanning(x)¶Return x times the hanning window of len(x).
Call signature:
window_hanning(x)
See also
window_none()window_none() is another window algorithm.matplotlib.mlab.window_none(x)¶No window function; simply return x.
Call signature:
window_none(x)
See also
window_hanning()window_hanning() is another window algorithm.